超详细 AlphaFold 3 算法解析
作者: 沈亦翀 (shenyichong2011@gmail.com), 马大程 (dachengma916@gmail.com)
最后更新: 2025年2月6日
主要参考文档
Input Preparation
MSA和Templates是如何来的?
- 为什么需要MSA?
- 存在于不同物种之间不同版本某一类蛋白,其序列和结构可能是相似的,通过将这些蛋白集合起来我们可以看到一个蛋白质的某些位置是如何随着进化改变的。
- MSA的每一行代表来自不同物种的相似蛋白。列上的保守模式可以反应出该位置需要某些特定氨基酸的重要性。不同列之间的关系则反应出氨基酸之间的相互关系(如果两个氨基酸在物理上相互作用,则他们在进化工程中氨基酸的变化也可能是相关的。)所以MSA经常用来丰富单一蛋白质的representation。
- 为什么需要Template:类似的,如果上述MSA中包含了已知的结构,那么那么它很有可能能够帮助预测当前蛋白质的结构。Template只关心单链的结构。
- 如何获取MSA?
-
使用genetic search搜索相近的蛋白质或者RNA链,一条链一般搜索出N_msa(<16384)条相近的链:
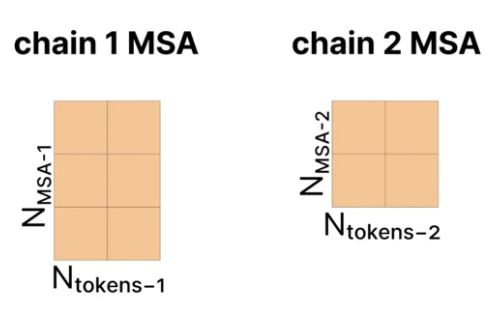
-
如果是多条链,如果来自相同物种可以配对(paired),那么MSA的矩阵可能的形式是这样的:
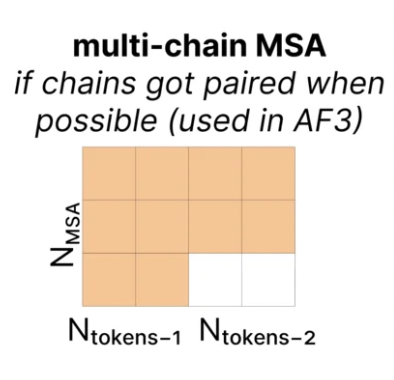
-
否则是这样的,构成一个diagnoal matrix:
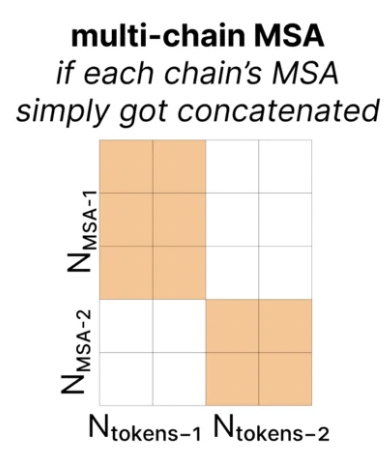
-
- 如何获取Template?
- 使用Template Search,对于生成的MSA,使用HMM去PDB数据库中寻找与之相似的蛋白质序列,接下来从这些匹配到的序列中挑选4个最高质量的结构作为模版。
- 如何表征Templates?
- 计算每一个token和token之间的欧几里得距离,并且是用离散化的距离表示(具体来说,值被划分为38个区间,范围从3.15Å到50.75Å,外加一个额外的区间表示超过50.75Å的距离)。
- 如果某些token包含多个原子,则选择中心原子用于计算距离,比如 Cɑ 是氨基酸的中心原子,C1是核苷酸的中心原子。
- 模版只包含同一条链上的距离信息,忽略了链之间的相互作用。
如何构建Atom-level的表征?
- 构建得到p和q:【对应Algorithm 5 AtomAttentionEncoder】
- 为了构建atom-level的single representation,首先需要所有的原子层面的特征,第一步是首先对每一个氨基酸、核苷酸以及ligand(配体)构建一个参考构象(reference conformer),参考构象可以通过特定的方式查出来或者算出来,作为局部的先验三维结构信息。
-
c 就是针对参考构象中的各个特征进行concate之后,再进行一次线性变换之后的结果。c的形状为[C_atom=128, N_atoms],其中C_atom为每一个atom线性变换之后的特征维度,N_atoms为序列中所有原子的个数。c_l代表l位置的原子的特征,c_m代表m位置的原子的特征。

-
atom-level的single representation q,通过c进行初始化:

- 然后使用c来初始化atom-level的原子对表征p(atom-level pair representation),p表征的是原子之间的相对距离,具体过程如下:
-
计算原子参考三维坐标之间的距离,得到的结果是一个三维的向量。

-
因为原子的参考三维坐标仅仅是针对其自身参考构象得到的,是一个局部信息,所以仅仅在token内部(氨基酸、核苷酸、配体等)计算距离,所以需要计算得到一个mask v,只有相同chain_id和residue_idx的情况下才相互之间计算坐标位置差异,这时候v为1,其他时候v为0

-
计算p,形状为[N_atoms, N_atoms, C_atompair=16]:

- p(l,m) 向量的维度为[C_atompair],计算方式为,对d(l,m)三维向量通过一个线性层,得到一个维度为C_atompair的向量,同时乘一个用于mask的标量v(l,m)。
- 在这里,inverse square of the distances 是一个标量,然后经过一个线性变换,变成[C_atompair]的向量,同时还是乘一个用于mask的标量v(l,m)。p(l,m) = p(l,m) + 这个新的向量。
- 最后,p(l,m)再加上mask这个标量。

- p(l,m) 还需要加上原始的c中的信息,包含c(:, l)的信息和c(:, m)的信息,这两个信息都先经过relu然后再做线性变换,变换成C_atompair的向量,加到p(l,m)中。
- 最后p(l,m) = p(l,m) + 三层MLP(p(l,m))
-
- 更新q(Atom Transformer):
- Adaptive LayerNorm:【对应Algorithm 26 AdaLN】
- 输入为c和q,形状都是[C_atom, N_atoms],c作为次要输入,主要用于计算q的gamma和beta的值,这样通过c来动态调整q的layerNorm的结果。
-
具体的来说,正常的LayerNorm是这样做的:
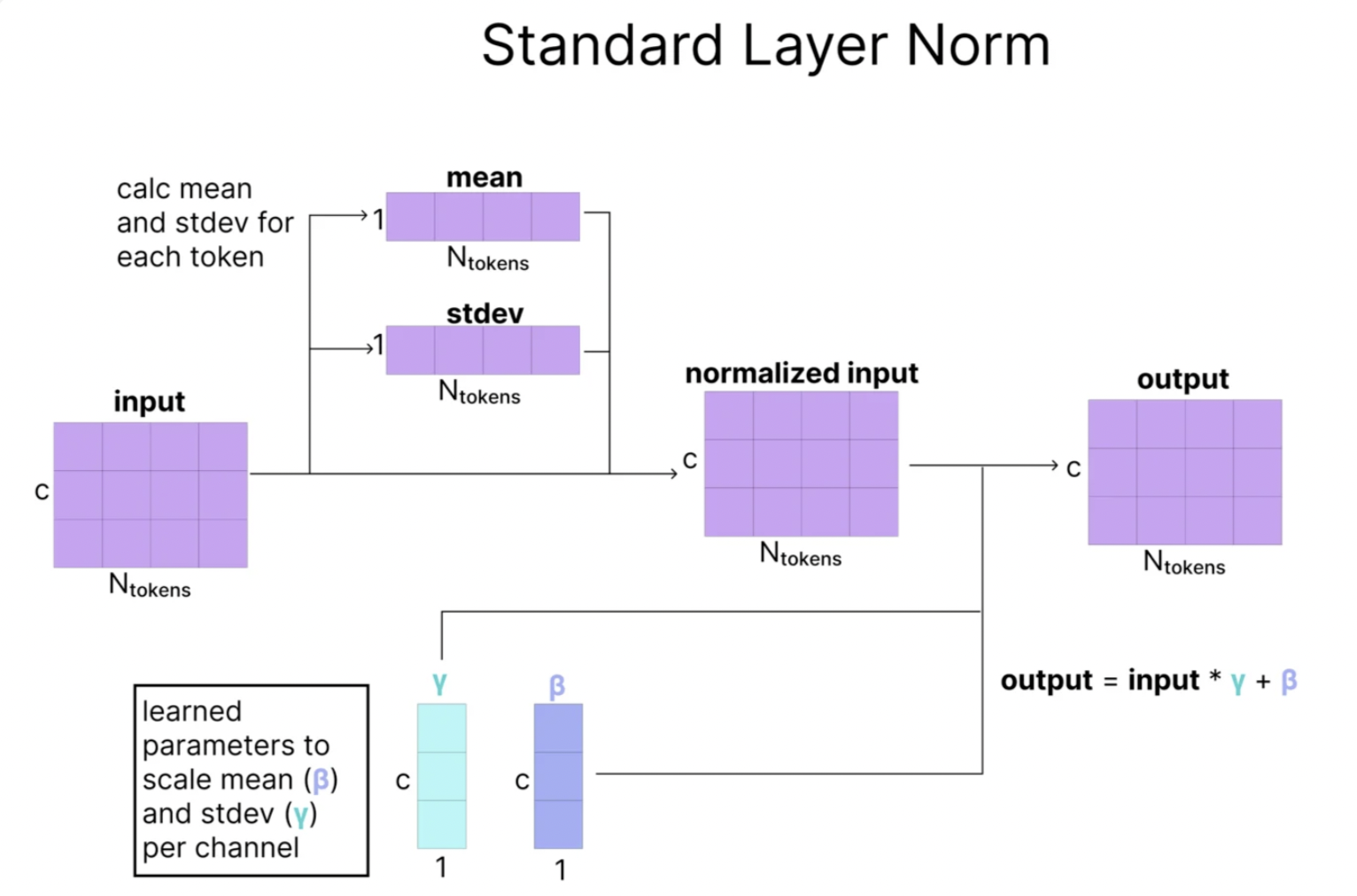
-
然后Adaptive Layer Norm是这样做的:
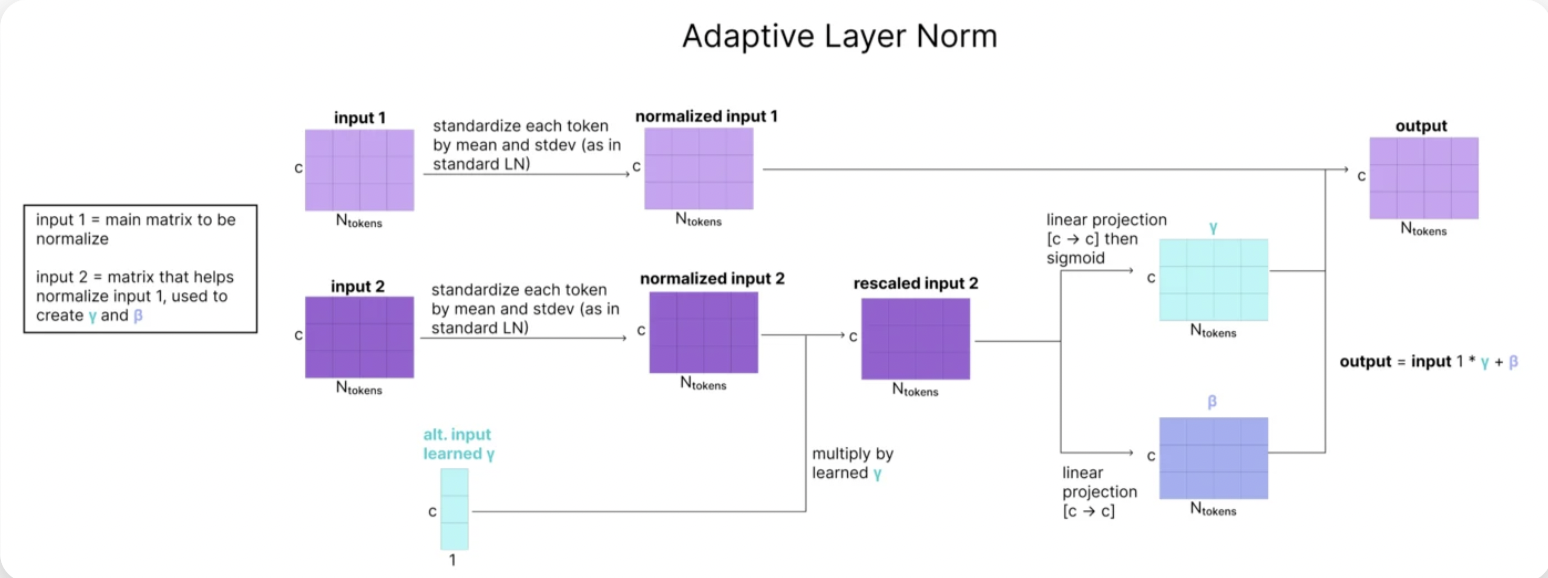
-
公式是这样的:

- 这里的a就是q,s就是c。
- 计算的时候sigmoid(Linear(s))相当于就是新的gamma,LinearNoBias(s)相当于就是新的beta。
-
- Attention with Pair Bias 【对应Algorithm 24 AttentionPairBias】:
- 输入为q和p,q的形状为[C_atom, N_atoms],p的形状是[N_atoms, N_atoms, C_atompair]。
- 作为典型的Attention结构,(Q, K, V)都来自于q,形状为[C_atom, N_atoms]。
-
假设是N_head头的attention,其中a_i代表q中的第i个原子的向量q_i,那么对于第h个头,第i个q向量,得到其(q_h_i, k_h_i, v_h_i):
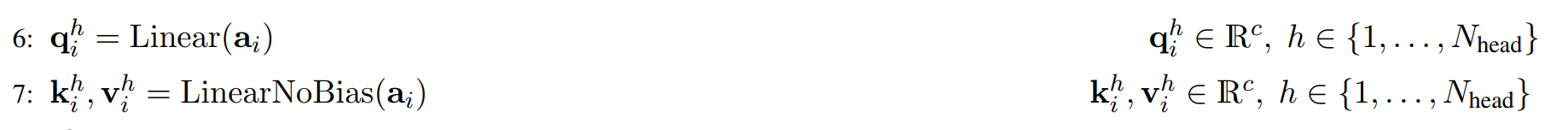
-
这里的维度c是这样得到的:
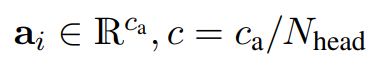
-
- Pair-biasing:从哪里来?从p中提取第i行,即第i个原子和其他原子的关系,那么p_i_j就是第i个原子和第j个原子之间的关系,向量形状为[C_atompair],在公式中使用z_i_j代表p_i_j。
-
z_i_j在C_atompair维度上先做了一次LayerNorm,然后再做一次线性变换,从C_atompair维降到1维:
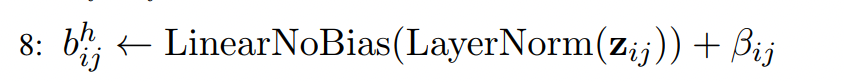
-
然后计算softmax之前引入此pair Bias,此时针对第i个原子和第j个原子的向量q_h_i和k_h_i先做向量点乘在scale之后,再加上一个标量b_h_i_j后进行softmax,得到权重A_h_i_j:
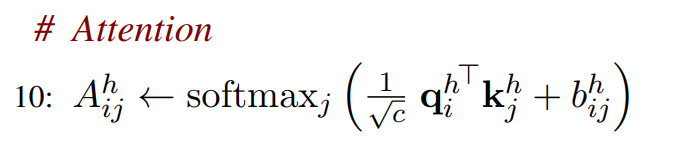
-
然后再直接计算对于第i个原子的attention结果:
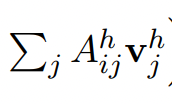
-
- Gating:从q中获取第i个原子的向量:
-
先做一次线性变换,从c_atom维变到Head的维度c上,然后再直接求sigmoid,将其映射到0到1之间到一个数上作为gating。

-
然后element-wise乘以attention的结果,最终将所有的Head concate起来,并最后经过一个线性变换,得到attention的结果q_i,形状是[C_atom]。
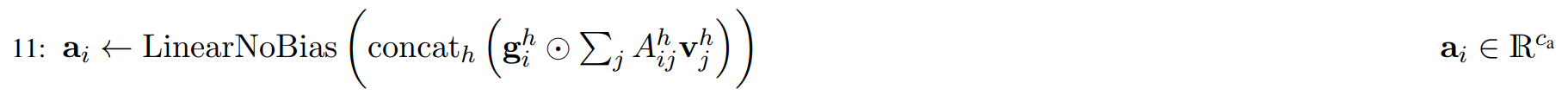
-
- Sparse attention:因为原子的数量远远大于tokens的数量,所以这里计算atom attention的时候,从计算量上来考虑,并不会计算一个原子对所有原子的attention,而是会计算一个局部的attention,叫做sequence-local atom attention,具体的方法是:
-
在计算attention的时候,将不关心位置(i,j)的softmax的结果做到近似于0,那么相当于在softmax之前特定位置(i,j)的值为负无穷大,通过引入的beta_i_j来进行区分:
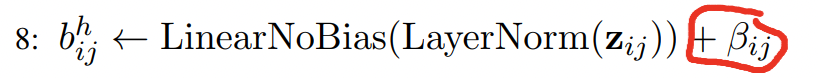
- 如果i和j之间的距离满足条件,那么就是需要计算atom attention的,这时候beta_i_j为0。
- 如果i和j之间距离不满足条件,那么就是不需要计算attention的,这时候beta_i_j为-10^10。
-
-
- Conditioned Gating: 【对应Algorithm 24 AttentionPairBias】
- 输入是c和q,形状分别是[C_atom, N_atoms], [C_atom, N_atoms],输出是q,形状是 [C_atom, N_atoms]。
-
这里公式中s_i实际上就是c_i ,先做一次线性变换,然后在计算sigmoid,将c_i中的每一个元素映射到0和1之间,最后在element-wise乘以a_i,实际上就是q_i, 得到最新的q_i:
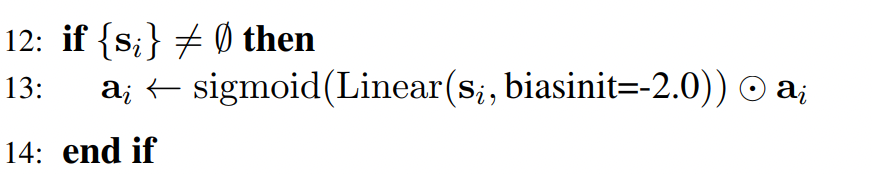
- Conditioned Transition: 【对应Algorithm 25 ConditionalTransitionBlock】
- 输入是c,q和p,形状分别是[C_atom, N_atoms], [C_atom, N_atoms], [N_atoms, N_atoms, C_atompair],输出是q,形状是[C_atom, N_atoms]。
- Atom Transformer的最后一个模块,这个相当于在Transformer中的MLP层,说他是Conditional是因为他包含在Adaptive LayerNorm层(前面第三步)和Conditional Gating(前面第三步)之间。区别只是中间的是MLP还是Attention。
-
第一步还是一个Adaptive LayerNorm:

-
第二步是一个swish:

-
第三步是Conditional Gating:
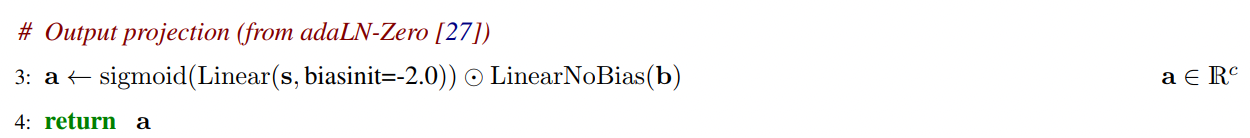
-
- Adaptive LayerNorm:【对应Algorithm 26 AdaLN】
如何构建Token-level的表征?
- 构建Token-level的Single Sequence Representation
- 输入是q,atom-level single representation,形状是[C_atom, N_atoms]。输出是S_inputs和S_init,形状分别是[C_token+65, N_tokens],[C_token, N_tokens]。
-
首先将每一个atom的表示维度C_atom经过线性变换到C_token,然后经过relu激活函数,然后在相同的token内部,对所有的atom表示求平均,得到N_token个C_token维度的向量。【来自 Algorithm 5 AtomAttentionEncoder】

-
然后针对有MSA特征的token,拼接上residue_type(32)和MSA特征(MSA properties:32+1),从而得到S_input。【来自 Algorithm 2 InputFeatureEmbedder】

-
最后再进行一次线性变换,从S_input转换为S_init。【来自 Algorithm 1 MainInferenceLoop】
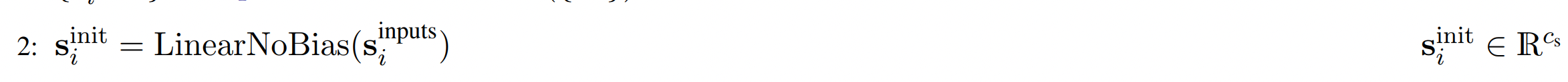
- 注意:这里的C_s就是C_token = 384
- 构建Token-level的Pair Representation 【来自 Algorithm 1 MainInferenceLoop】
- 输入是S_init,形状是[C_token=384, N_tokens],输出是Z_init,形状是[N_tokens, N_tokens, C_z=128]。
-
要计算Z_init_i_j,那么需要得到特定两个token的特征,将其分别进行线性变换之后,再相加得到第一个z_i_j,向量长度从C_tokens也就是C_s=384转换为C_z=128。
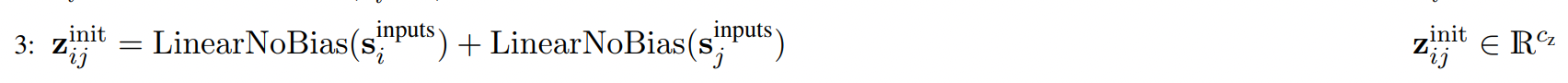
-
然后在z的(i,j)位置加入相对位置编码:

-
详解RelativePositionEncoding:注意这里的i和j都是指的token。【来自 Algorithm 3 RelativePositionEncoding】

- a_residue_i_j:残基相对位置信息:
- 如果i和j token在同一个链中,那么d_residue_i_j 则是i残基和j残基相对位置之差,范围在[0, 65]。
- 如果i和j token不在同一个链中,那么d_residue_i_j = 2*r_max+1 = 65
- a_residue_i_j 为一个长度为66的one-hot编码,1的位置为d_residue_i_j的值。
- a_token_i_j:token相对位置信息:
- 如果i和j token在同一个残基中,(对于modified 氨基酸或者核苷酸,那么一个原子是一个token),那么d_token_i_j 为不同残基序号之差,范围在[0, 65]。
- 如果i和j token不在同一个残基中,取最大值d_token_i_j = 2*r_max+1 = 65
- a_token_i_j 为一个长度为66的one-hot编码,1的位置为d_token_i_j的值。
- a_chain_i_j:链相对位置信息:
- 如果i和j token不在同一条链中,那么d_chain_i_j 为链之间的序号之差,范围在[0, 5]。
- 如果i和j token在同一条链中,那么d_chain_i_j设置为最大值5。
- a_chain_i_j为一个长度为6的one-hot编码,1的位置为d_chain_i_j的值。
- b_same_entity_i_j:如果i和j token在同一个实体(完全相同的氨基酸序列为唯一实体,拥有唯一实体id)中,为1否则为0.
- 最后将[a_residue_i_j, a_token_i_j, b_same_entity_i_j, a_chain_i_j] 拼接起来,得到了一个长度为66+66+1+6 = 139 = C_rpe 的向量。
- 然后再经过一次线性变换,将其向量维度变换到C_z=128维度。
- a_residue_i_j:残基相对位置信息:
-
-
最后在将token的bond信息加入,通过线性变换之后,加入z_i_j,得到最后的结果。
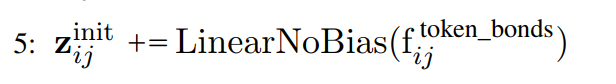
Representation Learning
Template Module
- Template Module的输入是什么?
- token-level pair representation { z_i_j } 和 包含template信息的特征 {f} 。
-
Template 特征如何构建?【来自 Algorithm 16 TemplateEmbedder】

- 针对template t,b_template_backbone_frame_mask_i_j 通过对第t个模版的i个位置和j个位置的template_backbone_frame_mask的值来计算,即只有i和j位置都包含了可以用于计算backbone的所有原子,此mask结果为1,否则为0.
- 同理,对第t个模版的i位置和j位置的template_pseudo_beta_mask都为1,此b_template_pseudo_beta_mask_i_j这个mask才为1,否则为0。含义是中心原子在i和j位置是否有坐标。
- a_t_i_j 计算第t个模版的i位置和j位置的相关特征,将template_distogram (表示两个token之间距离,形状为[N_templ, N_token, N_token, 39])的最后一维和b_template_backbone_frame_mask_i_j(1维标量),template_unit_vector(表示两个token之间包含方向的单位向量,形状为[N_templ, N_token, N_token, 3])的最后一维,和b_template_pseudo_beta_mask_i_j (1维标量) 拼接起来成为一个维度为44的向量。
- 如果位于i位置的token的和j位置的token不在一条链上,则a_t_i_j 向量设置为全0向量。
- a_t_i_j再拼接上位于t模版的i位置的残基类型(one-hot encoding) 和j位置的残基类型信息,得到a_t_i_j的向量为一个[44+32+32 =108]的向量。{a_t_i_j}的形状为[N_templ, N_token, N_token, 108]。
-
然后针对每一个template,做相同以下操作:【来自 Algorithm 16 TemplateEmbedder】

- 首先定义一个u_i_j用于存放结算结果,{u_i_j}的形状是[N_token, N_token, c]
- 针对每一个template,进行相同的操作:对a_t_i_j进行线性变换,从108维 → c维, 对z_i_j先进行LN,然后再进行线性变换,从c_z维 → c维,然后针对每一个template的a_t_i_j,都加上相同的z_i_j变换后的结果,得到v_i_j,维度为c维。
- 然后将v_i_j通过PairformerStack进行计算,得到的结果再加上v_i_j 作为v_i_j的结果,维度为c维。
- 最后对v_i_j 进行LN之后,对于所有的template都加到u_i_j向量上,维度为c维。
-
最后对u_i_j的结果进行平均,除以template的数量,最后再激活一下,然后经过一次线性变换得到最终的结果u_i_j, {u_i_j}的形状为[N_token, N_token, c] 。【来自 Algorithm 16 TemplateEmbedder】
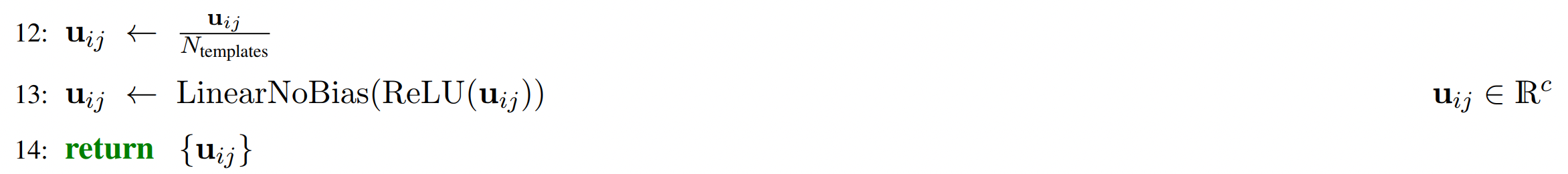
MSA Module
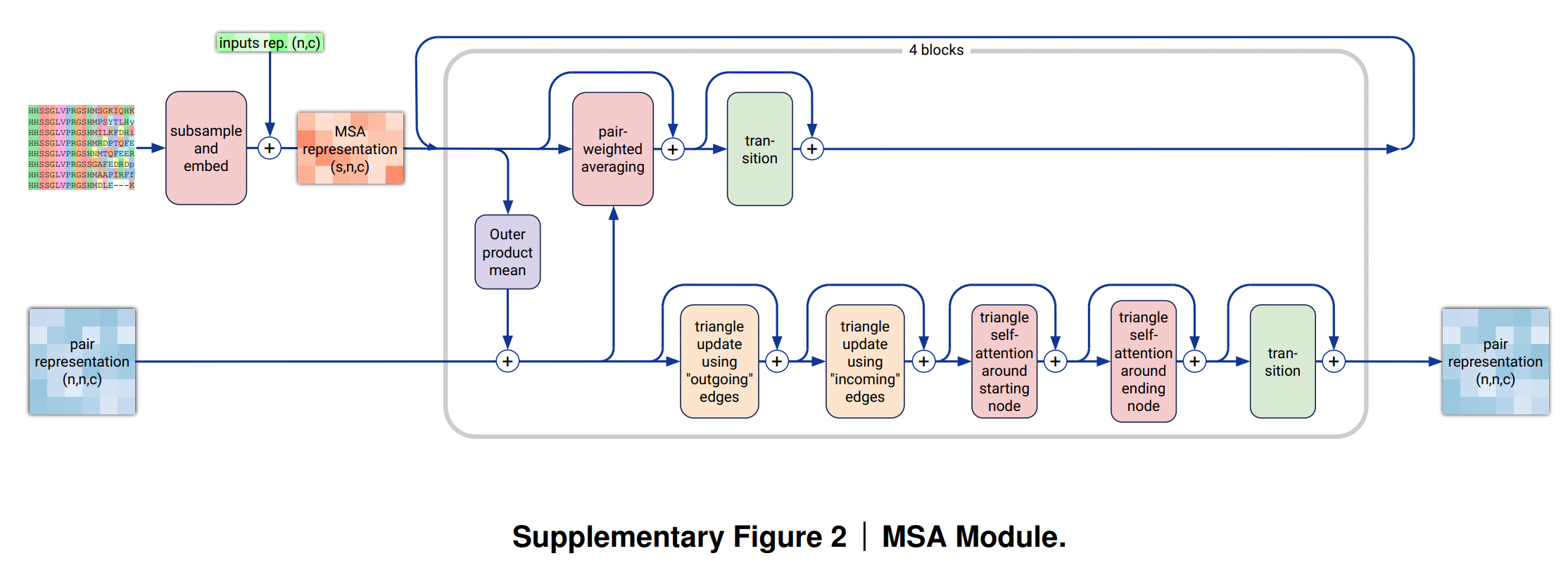
- 此模块的目标:同时更新MSA和Pair Representation特征,并让其相互影响。先通过Outer Product Mean来让MSA表征更新Pair Representation,然后再使用Pair Representation通过 row-wise gated self-attention using only pair bias来更新MSA的表征。最终Pair representation经过一系列的三角计算并最终进行更新。
- 输入:
- MSA 表征(会按照行进行subsamle,只随机选取其中少部分样本)
- f_msa: 形状为 [N_msa, N_token, 32],原始的N_msa条MSA样本,每一个位置有32种可能性。
- f_has_deletion: 形状为 [N_msa, N_token], 原始信息,指示每个位置左边是否有删除。
- f_deletion_value: 形状为 [N_msa, N_token],原始信息,指示Raw deletion counts,大小在[0,1]之间。
- S_inputs_i : 初始的token-level single sequence特征,形状为[N_token, C_token+65],这里的65是32+32+1,其中包含了当前token的restype,以及MSA的一些特征,包括在i位置的各个restype类型的分布,以及在i位置的deletion mean的值。如果当前token没有MSA信息,则这65维都为0.
- token-level Pair Representation:{z_ij} ,形状为[N_token, N_token, C_z=128]
- MSA 表征(会按照行进行subsamle,只随机选取其中少部分样本)
- 输出:更新之后的token-level Pair Representation:{z_ij} ,形状为[N_token, N_token, C_z=128]
-
直接看伪代码:

- 首先,通过对f_msa_Si,f_has_deletion_Si以及f_deletion_Si进行拼接,得到一个32+1+1=34的向量:m_Si。注意这里的S和i都分别是下标,S表示在N_msa中第S行(第S个样本),i表示每一行中第i个位置。
- 然后通过SampleRandomWithoutReplacement函数对N_msa进行subsample,{S}代表所有N_msa的可能的序号的集合,而{s}代表下采样之后的可能的序号的集合。
- 然后m_si代表的是针对下采样之后的样本的第s个样本第i个位置,然后进行线性变换,将维度从34→C_m=64。
- 然后加上{S_inputs_i} 进行线性变换后的结果得到一个新的MSA特征 m_si。这里S_inputs_i也包含了MSA在每一个位置上的相关特征(如果有的话),维度是 C_token+65。
- 然后针对N_block个block进行循环:
- 对MSA信息m_si进行OuterProductMean计算并融合到pair representation中:
-
输入{m_si}的形状是[n_msa, N_tokens, C_m],具体的算法如下:

- 首先,对m_si进行LN,{m_si}的形状为[n_msa, N_tokens, C_m]
- 然后进行线性变换,得到a_si和b_si,线性变换是从C_m=64 → c=32
- 对于每一个s,计算a_si和b_sj的外积,相当于计算对于s这个MSA样本来说,计算其i位置和j位置的关系,通过外积来计算。
- 长度为c的向量与长度为c的向量的外积的计算得到一个[c , c]矩阵,
- 然后将s个[c, c]的矩阵按每个位置(i,j)求平均,
- 最后将这个矩阵变成一个一维向量,得到o_ij,形状为c*c。
- 最后在经过一次线性变换,将c*c → c_z=128 维度,得到最终的z_ij,即通过MSA计算得到位置之间的信息。
注1:这里通过OuterProductMean方法,将MSA的表征融合到pair representation中去。对于同一个MSA序列,通过外积的方式得到其任意两个位置之间的关系,然后对所有的MSA序列的这两个位置的结果求平均,得到任意两个位置之间在进化上的关系信息并融合到pair representation中去。
注2:注意到这里是仅仅在进化序列内部进行计算,然后进化序列之间的信息是唯一一次通过平均的方式融合在一起,避免了AF2中进化序列之间复杂的计算。
-
- 使用更新后的pair representation和m_si来更新m_si(MSA特征): MSA row-wise gated self-attention using only pair bias
-
输入是{m_si}的形状是[n_msa, N_tokens, C_m=64], {z_ij}的形状是[N_token, N_token, C_z=128]。输出是{m_si},形状是[n_msa, N_tokens, C_m=64]。具体的算法如下:

- 首先对MSA特征m_si进行LN。
- 然后对m_si进行多头线性变换,得到H_head个头v_h_si,线性变换维度从C_m→ c。
- 对pair represnetation特征z_ij首先进行LN,然后进行多头线性变换,得到b_h_ij,维度从C_z→1。
- 对m_si进行多头线性变换,维度从C_m→c,然后计算其sigmoid的值,得到g_h_si,用于后续做gating。
- 对b_h_ij沿着j的方向做softmax,得到weight w_h_ij,维度为1。
- 这里比较难理解的是如何得到o_h_si,这里v_h_sj和w_h_ij在j方向上按元素相乘,然后加起来得到o_h_si的中间结果。
- 即通过对于{w_h_ij}这个形状为[N_token, N_token]的矩阵,取其第i行的元素[N_token]。
- 对{v_h_sj}这个形状为[n_msa, N_token, c]的矩阵取其第s行的元素[N_token, c]。
- 将其进行按元素相乘并加总起来,得到一个c维度的向量,其的位置为原来{m_si}矩阵的s行和i列。
- o_h_si 再在c维度上按元素乘以g_h_si,进行gating。
- 最后针对o_h_si,将其H_head个头concate起来,得到一个c*H_head长的向量,然后经过线性变换后得到最终结果m^_si。
-
注意,这部分是通过pair representation来更新MSA的表征,更新方式是对每一个MSA的序列来说,其更新是相互独立的。然后使用pair representation中的位置之间的关系来构建weight,相当于给m_si中的每一个位置做了一次self-attention,引入了pair representation中的信息。
-
- {m_si} 再经过一层transition层后再作为下一个block的{m_si}的输入。
- pair representation {z_ij}经过一系列的三角计算和transition后,再作为下一个block{m_si}的输入。
- 对MSA信息m_si进行OuterProductMean计算并融合到pair representation中:
Pairformer Module
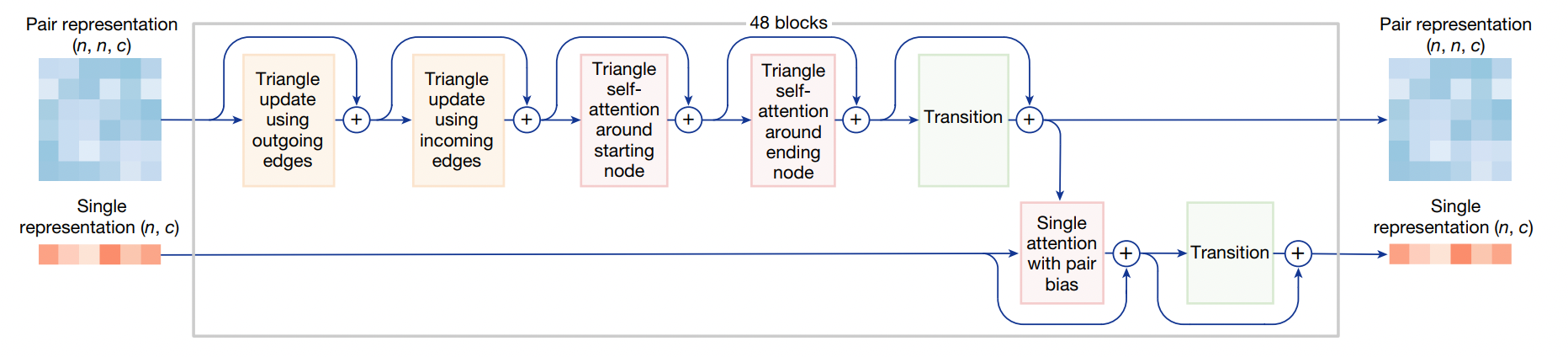
- 首先了解Pairformer这部分模块主要做了什么事情:Pair Representation会进行三角更新和三角注意力计算,并且用于更新Single Representation。和AF2不同的是,这里Single Representation不会去影响Pair Representation。
- 输入输出:输入是token-level pair representation {z_ij} 和 token-level single representation {s_i} ,他们的形状分别是[N_token, N_token, C_z=128] 和 [N_token, C_s=C_token=384]。
- 为什么要关注三角关系?(Why look at Triangles?)
- 三角不等式说:三角形任意两边之和大于第三边。而在pair representation 中表征了任意两个token之间的关系,为了简化理解,我们可以将其看作是一个序列中任意两个氨基酸之间的距离,那么z_ij代表i氨基酸和j氨基酸之间的距离,那么已知z_ij=1, z_jk=1,那么我们就可以知道z_ik < 2。这样我们可以通过z_ij和z_jk的距离来确定z_ik的距离的范围,也就是说可以通过z_ij和z_jk来约束z_ik可能的值,故三角更新和三角注意力机制就是为了将这种几何约束编码到模型之中。
- 所以,z_ij的值可以通过获取所有可能的k得到的(z_ik,z_jk)来进行更新,由于真实情况是,z_ij并不仅仅包含了距离信息,它代表了i和j之间的关系信息,因此它也是有方向的,z_ij和z_ji表示的含义是不一样的。
-
并且基于图(graph)计算理论,将三角关系中,用于更新z_ij这一条边的另外两边的方向分为incoming和outgoing。则针对z_ij,
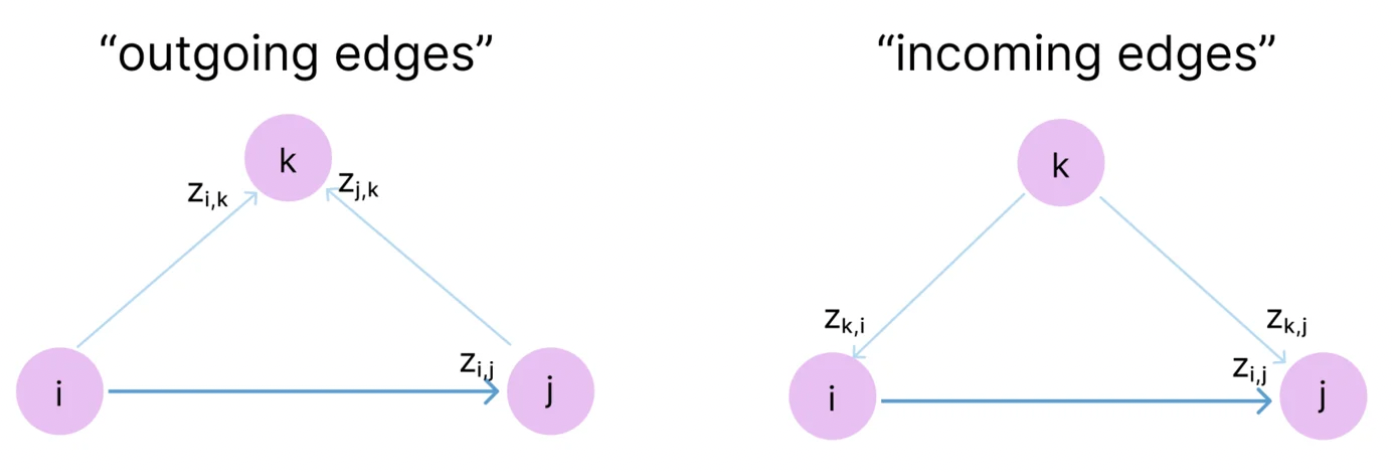
- 其outgoing edges是:z_ik, z_jk
- 其incoming edges是:z_ki, z_kj
- 为什么要区分outgoing edges和incoming edges?为什么不能混用? → 当前暂时的理解是,两条边同时从i和j指向k或者同时从k指向i和j,因为edge是有方向性的,同时从i和j指向k或相反,这两条边的物理含义是一致的,就是i和j对k的关系(或相反),更加便于模型准确地建模。(这里的理解还是不够透彻,等有机会再梳理。)
- 接下来看看具体是如何计算trianglar update和triangular attention是如何计算的:
- Triangular Update
- Outgoing:
-
具体的算法实现:

- z_i_j 这个向量,自己进行LayerNorm,即在c_z维度上进行归一化。
- z_i_j进行线性变换,转换为维度为c=128的向量,然后每一个位置计算sigmoid的值,然后和另外一个进行了线性变换的向量进行按元素相乘,得到一个a_i_j 或者b_i_j,维度是c维。
- 然后还是对z_j_j先进行线性变换(变换维度不变,还是c_z),然后计算sigmoid,得到g_i_j,维度是c_z,这个向量用于gating。
- 最后,计算Triangular Update,要更新z_i_j,那么需要从a_i_k和b_j_k的计算中得到(k有N_token个选择)。具体方法是:那么从{a_i_j}中选取i行,得到{a_i}(有N_token个向量),从{b_i_j}中选取j行,得{b_j}(有N_token个向量),然后对{a_i}和{b_j}中的第k个元素,计算按元素相乘,得到一个c维的向量,然后再将所有的N_token个向量加起来,得到一个c维度的向量,然后进行LayerNorm计算,最后进行线性变换得到一个c_z维度的向量;最后按照元素相乘g_i_j,得到最终的z_i_j的结果。
-
图示化解释:
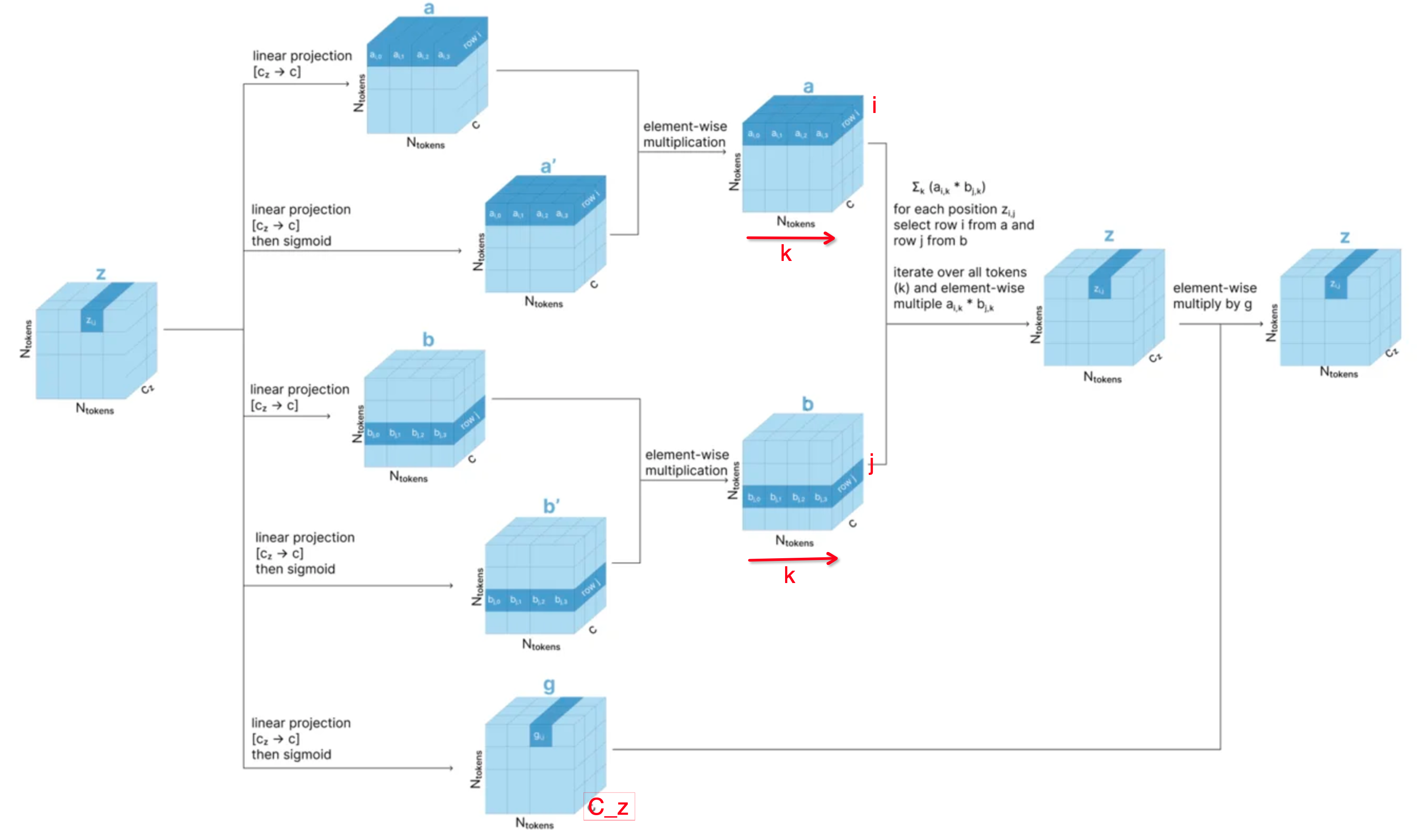
-
- Incoming:
-
具体的算法实现:

- 注意这里的主要变化,就是计算的是a_k_i和b_k_j,即从列的角度进行计算,和前面的计算方法刚好对称。从下面的图示也可以明显的看出来。
-
图示化解释:
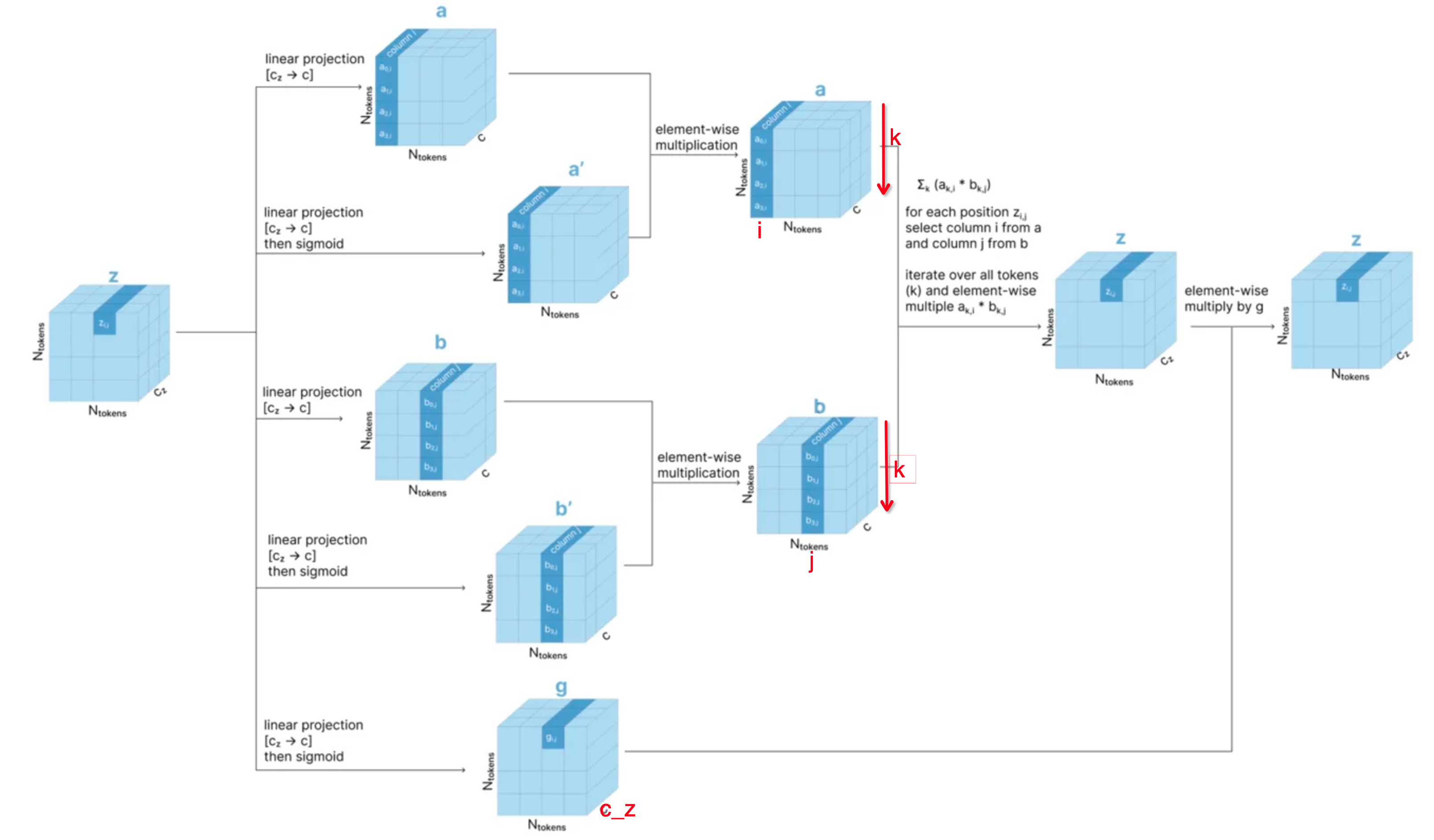
-
- Outgoing:
- Triangular Attention
- Triangular Attention (Starting Node 对应outgoing edges)
-
具体算法实现:

- 首先对z_i_j 进行LayerNorm归一化处理。
- 针对N_head个头的特定h头,对z_i_j进行不同的线性变换,得到q_h_i_j, k_h_i_j, v_h_i_j,维度变换均为c_z → c。
- 针对N_head个头的特定h头,对z_i_j进行线性变换,得到b_h_i_j。维度变换为c_z → 1。
- 针对N_head个头的特定h头,对z_i_j先进行线性变换,维度变换为c_z → c,然后每一个元素计算sigmoid的值,得到g_h_i_j用于后续的gating。
- 计算Triangular Attention 第一步:计算attention score,针对q_h_i_j和k_h_i_k计算点积,然后再除以sqrt(c),然后再加上b_h_j_k这个维度为1的值,得到的一个标量再在k维度上计算softmax的值,得到在k位置上的attention score a_h_i_j_k。这是一个标量值,页可以理解是一个weight的值,用于后续乘以value。
- 计算Tiangular Attention 第二步:计算(i,j)位置上的attention的结果,通过a_h_i_j_k 与 v_h_i_k 的weighted sum,得到attention在(i,j)位置上的值,这是一个维度为c的向量;然后与g_h_i_j进行按元素相乘,得到gating之后的attention向量o_h_i_j,维度也为c。
- 最后针对{i,j}位置的值,将多头进行合并,首先按照h个多头,在最后一个特征维度进行拼接,维度变化:c → hc;然后再进行一次线性变换,将维度从 hc → c 得到最终的结果z_i_j。
-
图示化解释:
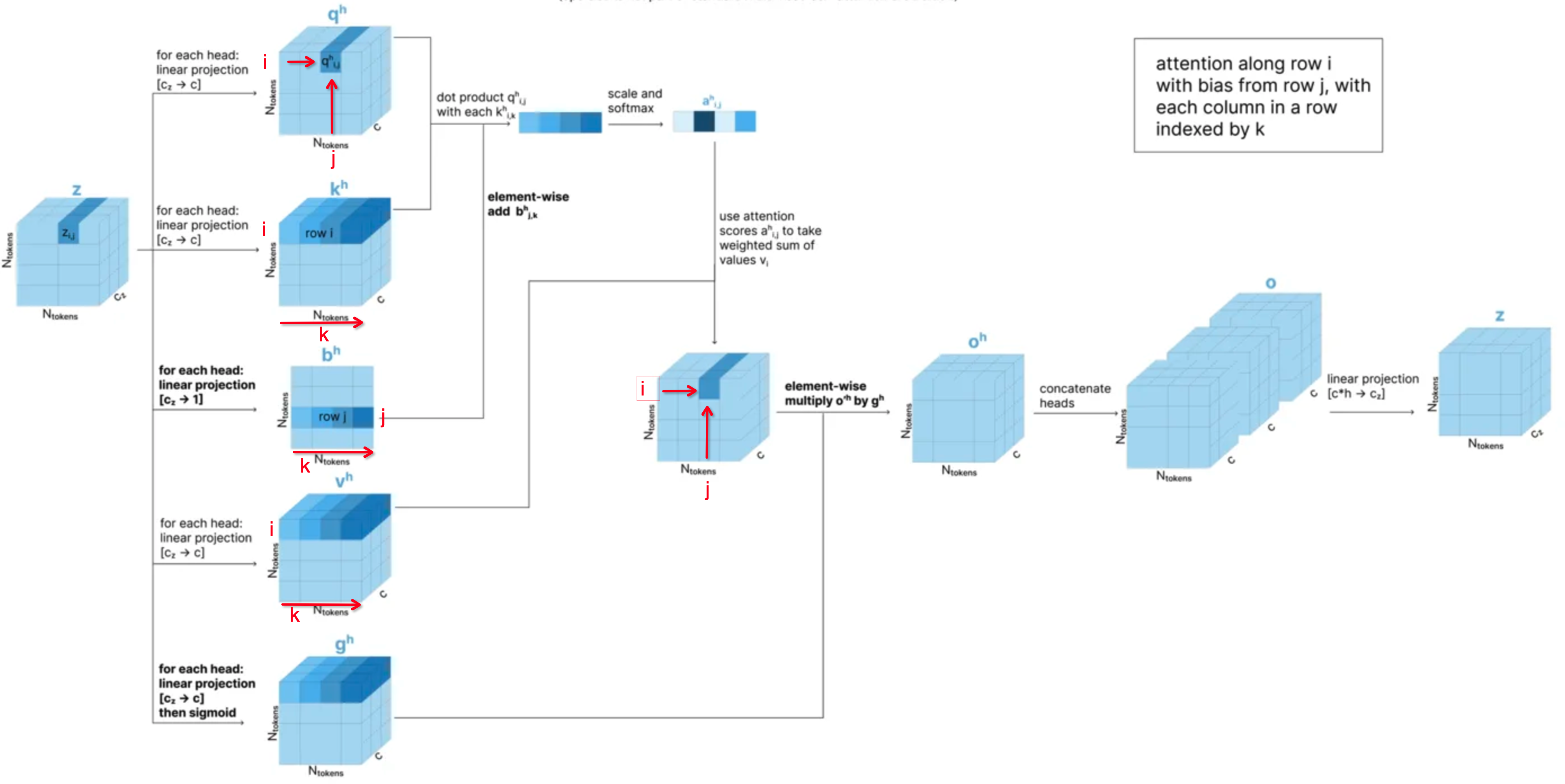
- 这里注意,其实这里的Triangular Attention就是一种Axial Attention的变种,增加了b_j_k作为bias,增加了gating的机制。但是如果抛开这两个增加到特性,相当于是按行在做self-attention。
-
- Triangular Attention (Ending Node 对应incoming edges)
-
具体算法实现

- 这里的主要区别在计算Triangular Attention的方法:
- 使用q_h_i_j 和 k_h_k_j 来计算attention score,然后再加上b_h_k_i 这个偏置,作为a_h_i_j_k的结果。这里需要注意的是q_h_i_j是和k_h_k_j而不是和k_h_k_i来求点积,加上的是b_h_k_i而不是b_h_k_j。原因我猜测是为了方便还是计算Axial Attention,否则就不是基于列的self-attention了。具体可以见下面图示。
- 这里的主要区别在计算Triangular Attention的方法:
-
图示化解释
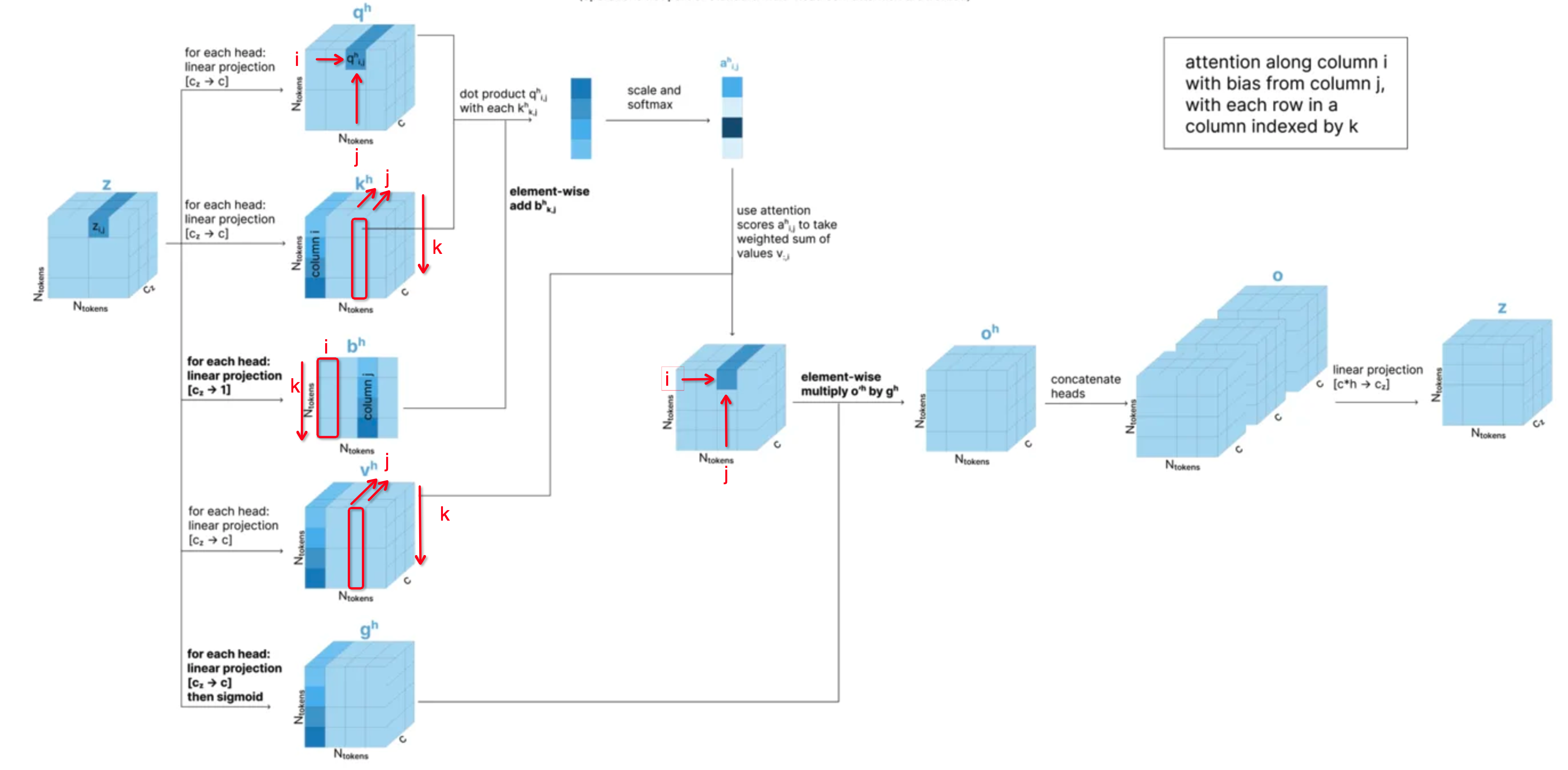
- 原来的图解是错误的,其并没有忠实按照官方文档中的实现进行图示,红色框部分修改了原来途中的错误标注。
-
- Triangular Attention (Starting Node 对应outgoing edges)
- Triangular Update
- 最后看看Single Attention with pair bias 如何实现。
- 输入是token-level single representation {s_i} 和token-level pair representatoin {z_i_j} , 输出是{s_i}。
- 主要使用{z_i_j}作为偏置,加入到{s_i}的self-attention计算中,同时{s_i}的self-attention中也增加了gating的机制。
-
具体算法伪代码实现为:

- single representation {s_i} 进行归一化计算。
- 从{s_i} 计算特定h头的q、k、v表示:q_h_i , k_h_i, v_h_i 都经过了线性变换从c_token → c。
- 从pair representation {z_i_j} 中计算一个偏置的值,准备应用在{s_i}的self-attention中:首先{z_i_j}进行归一化,然后进行线性变换,维度从c_z → 1 ,得到b_h_i_j。
- 使用{s_i}计算后续用于gating的值:先对{s_i}进行线性变换c_token → c ,然后对于其中的每一个元素计算sigmoid的值,得到g_h_i。
- 然后计算attention,实际上就是正常的self-attention,只是在计算attention score的时候,加入了来自于pair representation的偏置的值b_h_i_j,从而得到标量,A_h_i_j。
- 然后使用v_h_j对每一个j乘以A_h_i_j,并求和,得到一个经过weighted sum的向量,然后再按元素乘g_h_i,得到特定h头上的attention结果,然后将其结果按照最后一维拼接起来,并最终通过一个线性变换,得到经过attention之后的{s_i}的结果,维度为c_token。
-
具体的图示化解释如下:
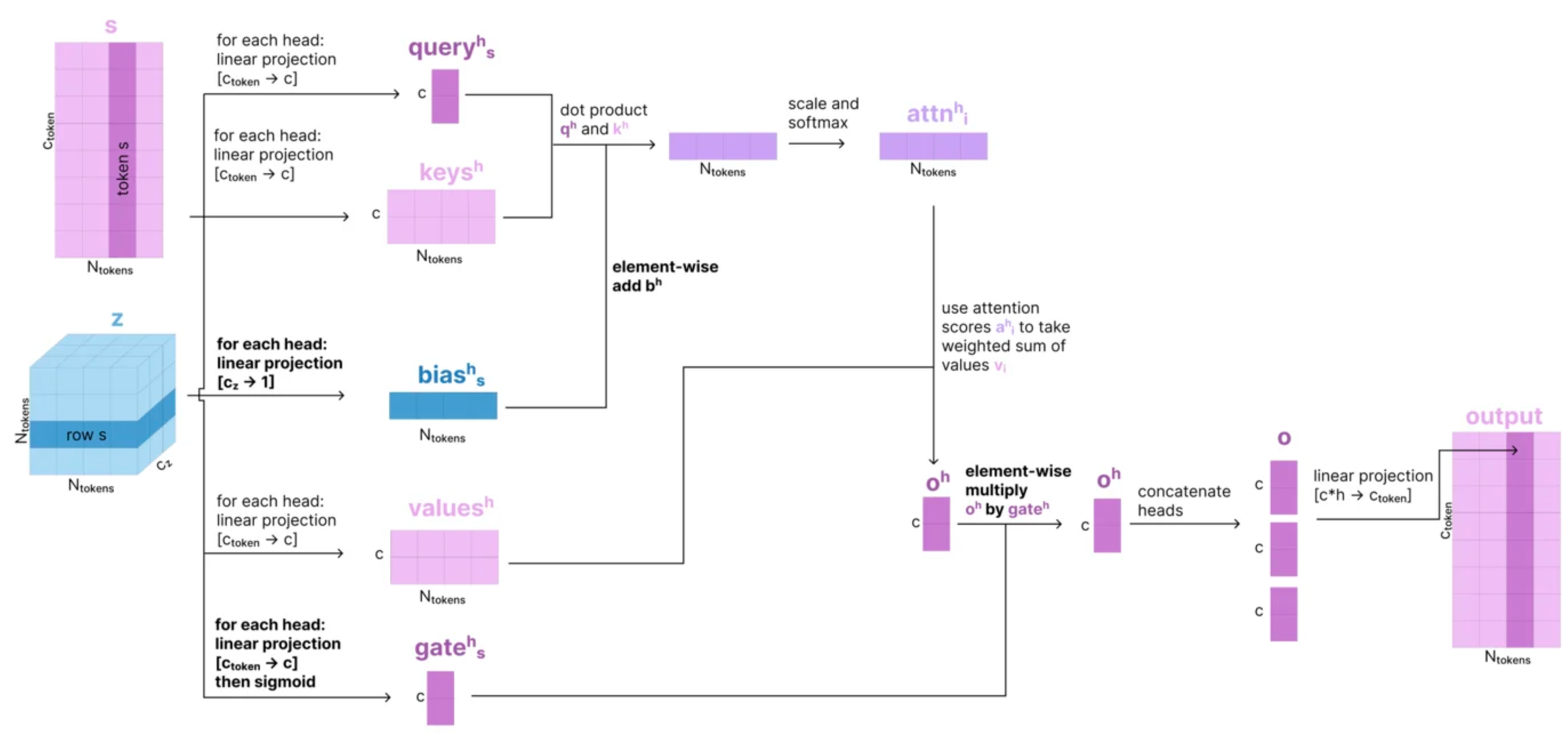
Structure Prediction
Diffusion的基本概念
- 在Alphafold3中整个的结构预测模块采用的方法是atom-level的diffusion。简单来讲,diffusion的具体是按照如下方式工作的:
- 从最真实的原始数据开始,假设是一张真实的熊猫照片,然后呢不断对这张照片加入随机噪声,然后训练模型来预测加入了什么样的噪声。
- 具体的步骤如下:
- 训练阶段:
- 加噪声过程:
- 假设x(t=0)是原始的数据,在第一个时间步,对数据点x(t=0)添加一部分噪声,得到x(t=1)。
- 在第二个时间步,对x(t=1)添加噪声,得到x(t=2)。
- 持续重复这个过程,经过T步之后,数据完全被噪声覆盖,成为随机噪声x(t=T)。
- 模型的目标:给定某一个被噪声污染的数据点x(t)和时间步t,模型需要预测这个数据点是如何从上一步x(t-1)转变而来,即模型需要预测在x(t-1)到x(t)添加了什么噪声。
- 损失函数:模型的预测噪声和实际添加的噪声之间的差异。
- 加噪声过程:
- 预测阶段:
- 去噪声的过程:
- 从纯随机噪声开始,x(t=T)是完全随机的噪声。
- 在每一个时间步t,模型预测这一步应该移除的噪声,然后去除这些噪声,得到x(t-1)。
- 重复这一过程,逐步从x(t=T)移到x(t=0)。
- 最终得到一个去噪声之后的数据点,应该看起来像训练数据。
- 去噪声的过程:
- 训练阶段:
- 什么是条件扩散(Conditional Diffusion)?
- 在扩散模型中,模型还可以基于某些输入信息来“控制”生成的结果,这就是条件扩散。
- 所以不论在训练还是预测的过程中,在每一个时间步上,模型的输入应该包括:
- 当前的在t时刻的数据点x(t)。
- 当前的时间步t。
- 条件信息(如蛋白质的属性等信息,这里主要还是指的token-level和atom-level的single和pair representation 作为条件信息)。
- 模型的输出:预测的从x(t-1)到x(t)添加到噪声(训练),或者,预测从x(t)到x(t-1)应该移除的噪声(推理)。
-
Diffusion如何在Alphafold3中进行应用?
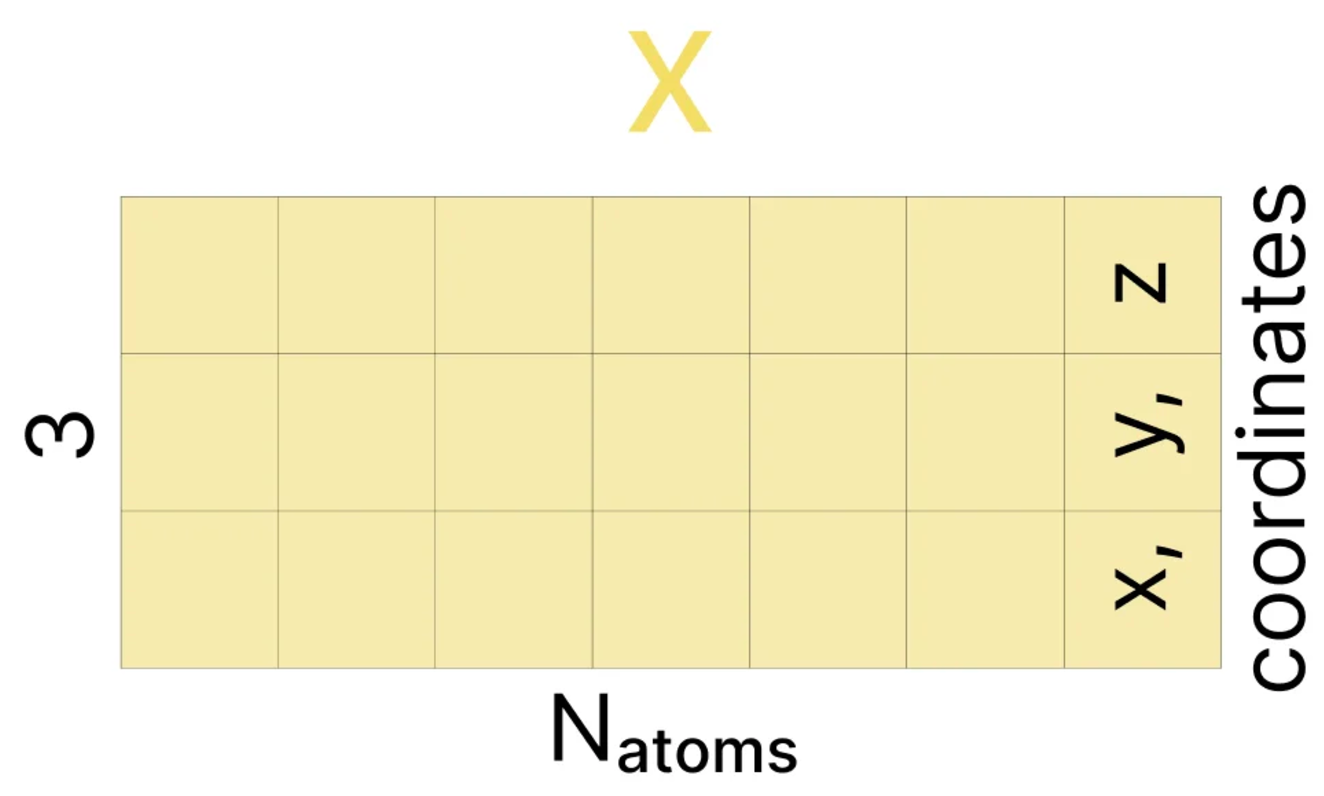
- 在Alphafold3中,用于去噪的原始数据为一个矩阵x,它的维度为[N_atoms, 3],其中3是每一个原子的坐标xyz。
- 在训练的时候,模型会基于一个正确的的原子三维坐标序列x,在每一步进行高斯噪声的添加,直到其坐标完全随机。
- 然后在推理的时候,模型会从一个完全随机的原子三维坐标序列出发,在每一个时间步,首先会进行一个data-augmentation的操作,对三维坐标进行旋转和变换,目的是为了实现在AF2中的Invariant Point Attention(IPA)的功能,证明经过旋转和变换之后的三维坐标是相互等价的,然后会再向坐标加入一些噪声来尝试产生一些不同的生成数据,最后,预测当前时间步降噪之后的结果作为下一步的起点。
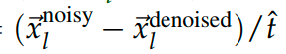
Structure Prediction 详解
Sample Diffusion部分详解(推理过程)
- 基本的扩散过程在alphafold3中的应用,这里是指的diffusion模型的推理过程在alphafold3的推理过程中的具体算法流程,从初始状态(完全随机的三维结构),然后经过一步一步地去噪,最终返回一个去噪之后的结果(预测的三维结构)。
-
具体的算法伪代码以及解析如下所示:

- 首先它的输入参数包括了很多后续用于conditional diffusion的输入,包括f*,{s_inputs_i}, {s_trunk_i}, {z_trunk_i_j} ,这些后续主要在DiffusionModule这个算法中进行处理,这里暂时忽略不讨论。
- 其他的输入主要是diffusion算法中所需要关注的输入,包括Noise Schedule $[c_0, c_1, …, c_T]$,缩放因子( $γ_0$ 和 $γ_{min}$),噪声缩放系数 noise_scale $λ$ ,和步长缩放系数 step_scale η。他们的具体作用介绍如下:
- Noise Schedule(噪声调度表):定义了扩散过程中每一步的噪声强度,取值范围是[0,1]之间,它是预先设定好的一系列标量。一般情况下,噪声强度从t=0时候为最大,然后慢慢减小,到较小的t=T时候结束。
- 缩放因子( $γ_0$ 和 $γ_{min}$),噪声缩放系数 noise_scale $λ$ ,都是用在Sample Diffusion的推理每一步开始时,需要给上一个step的迭代结果先添加噪声,生成噪声 $\hat\xi_l$ 的作用。
- 步长缩放系数 step scale η:主要是用于在后续x_l进行更新的时候,控制每一步迭代中输入更新的幅度,在x_l进行更新的过程中 $\vec{x}_l \leftarrow \vec{x}_l^{\text{noisy}} + \eta \cdot dt \cdot \vec{\delta}_l$ :如果η > 1 则增大更新幅度,加快去噪过程;如果η < 1 则减小更新幅度,使得去噪过程更平滑,但是可能需要更多迭代步数。
- 具体的算法流程解析如下:
- 最初的时候, $\vec{x}_l$ 是完全随机的三维噪声,维度是[3],{$\vec{x}_l$ }的维度是[N_atoms, 3]。其中 $\mathcal{N}(\vec{0}, \mathbf{I}_3)$ 是多维正态分布,均值为三维向量 [0,0,0], 表示三个维度的均值都是0;协方差矩阵为[1, 0, 0; 0, 1, 0; 0, 0, 1],表示各个维度之间相互独立且方差都为1.
- 接下来进入每一个时间步的循环,从 $\tau=1$ 开始直到 $\tau=T$:
- 首先进行一次数据增强,这里的目的是为了解决之前Alphafold2中使用Invariant Point Attention方法要去解决的问题,即解决旋转不变性和平移不变性,即一个序列的三维结构的坐标通过随机旋转和平移后实际上得到的新的坐标是等价的,三维结构本质不变,原子和原子之间的相对位置不变。
- 一般情况下,$c_\tau < \gamma_{\text{min}}$,因为这里的 $\gamma_{\text{min}} = 1$,所以 $\gamma=0$.
- 所以,这里的时间步 $\hat{t} = c_{\tau-1}$。
- 计算得到的加噪声为: $\vec{\xi}_l = 0*(\vec{0}, \mathbf{I}_3)$,并没有加什么噪声。
- 于是得到加了噪声最后的 $\vec{x}_l^{\text{noisy}} = \vec{x}_l$
- 这时候调用DiffusionModule(下一阶段会详解)计算真正此步推理的结果,得到去噪之后的结果 ${\vec{x}_l^{\text{denoised}}}$。
- 然后开始计算去噪方向的向量 $\vec{\delta}_l = \frac{\left( \vec{x}_l^{\text{noisy}} - \vec{x}_l^{\text{denoised}} \right)}{\hat{t}}$,即加噪声坐标 $\vec{x}_l^$距离去噪坐标 $\vec{x}_l^{\text{denoised}}$的方向和幅度,然后进行噪声归一化,使得去噪方向在每一个时间步的噪声强度变化中保持稳定。可以将其理解为扩散过程中类似于”梯度“或者“方向导数”
- 然后计算时间步差值dt,当前时间步和之前时间步的差值,为更新提供了一个“步长”,从 $c_\tau$到前一个时间步参数 $\hat{t}$ 的差值,这里实际上正好就是 $dt = c_\tau - c_{\tau-1}$。
- 最后,更新 $\vec{x}_l$,从加噪声的坐标开始 $\vec{x}_l^{\text{noisy}}$ 其实这里就是 $\vec{x}_l=\vec{x}_l+\eta \cdot dt \cdot \vec{\delta}_l$ 。由于这里dt大概率是一个负数,所以实际上是减去噪声。
Diffusion Module部分详解(推理过程)
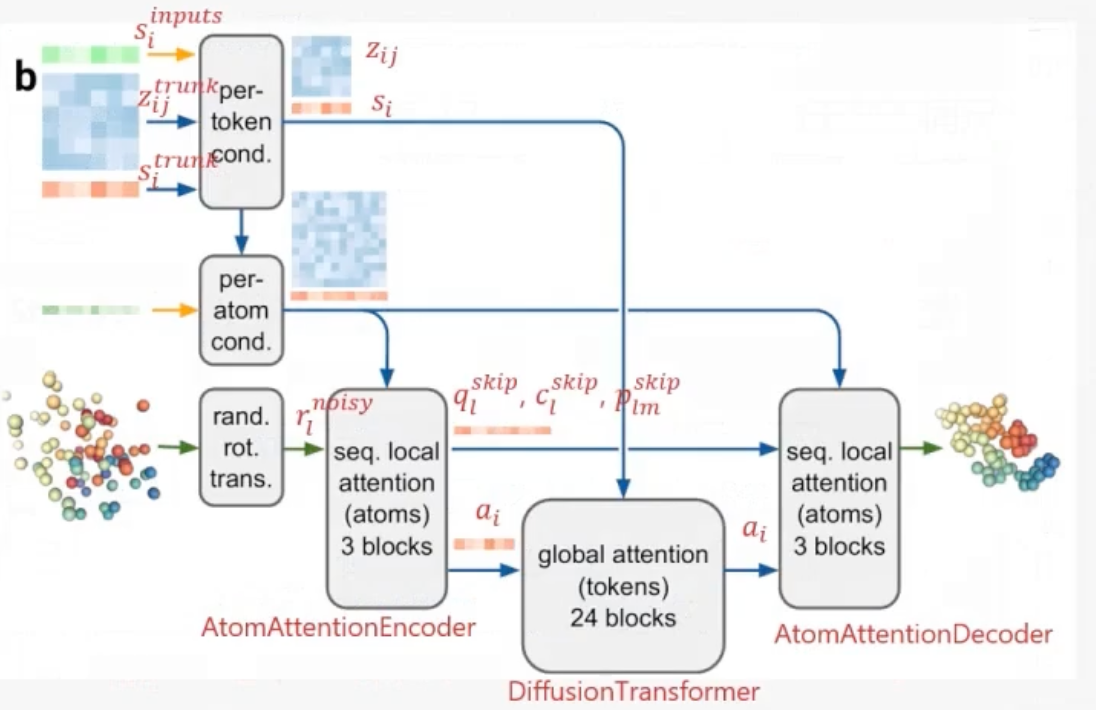
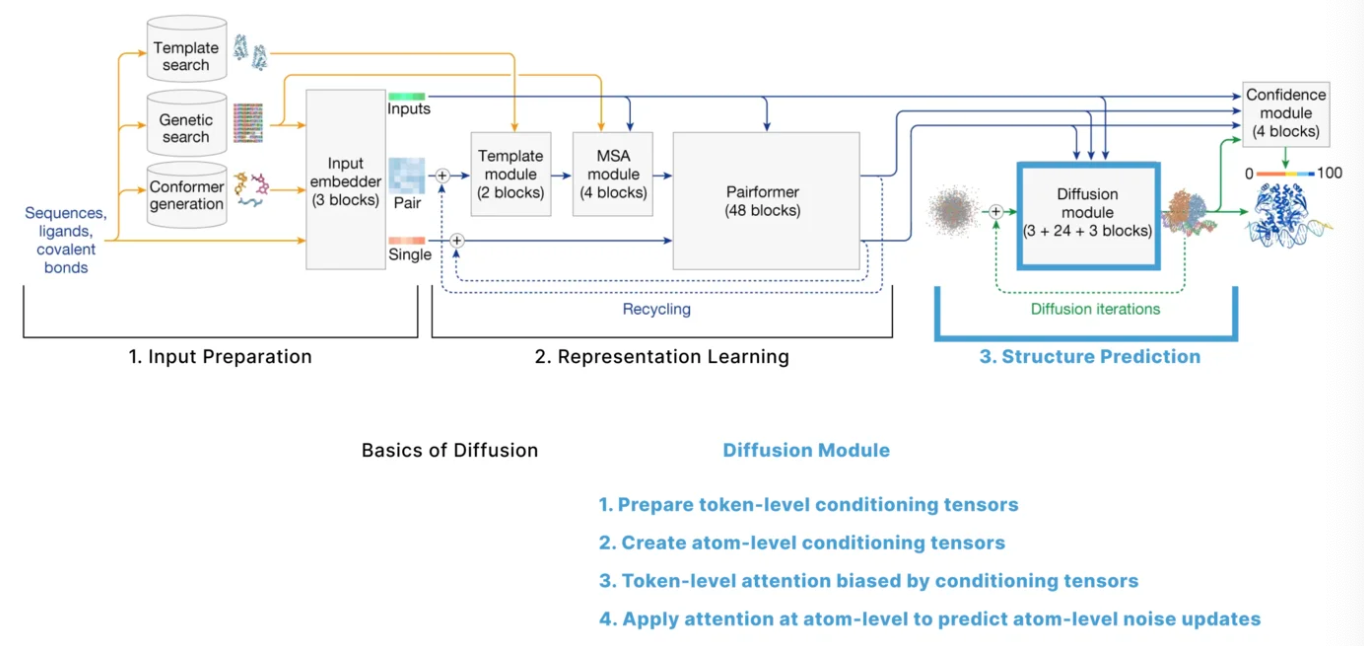
- DiffusionConditioning : 准备token-level的 conditioning tensors ( pair表征 z_i_j 和 single 表征 s_i )
- AtomAttentionEncoder : 准备atom-level的conditioning tensors (pair 表征 p_l_m, single表征 q_l, c_l),同时使用其生成token-level的 single 表征 a_i。
- DiffusionTransformers:token-level的single表征 a_i 经过attention计算,然后映射回 atom-level。
- AtomAttentionDecoder:在atom-level上进行attention计算,得到预测的atom-level的降噪结果。
注1:这里Atom-level的attention都被作者标注为local attention,token-level的attention都被作者标注为global attention,原因在于原子的数量非常大,在计算原子序列之间的attention的时候,也就是计算AtomTransformer的时候,实际上都是计算的稀疏注意力,距离当前的query原子距离过远的其他原子并不参与当前原子的attention计算,否则计算量会非常大,所以它叫做local attention。而在token-level的attention计算的时候,则是考虑了整个全局的所有token的信息,所以叫做global attention。
注2:这里的AtomAttentionEncoder中 3 blocks 和AtomAttentionDecoder 中的 3 blocks,指的就是AtomTransformer,本质上是加上稀疏偏置之后的在原子粒度上的DiffusionTransformer,而在token粒度上的DiffusionTransformer是24个blocks。
- DiffusionConditioning
-
算法伪代码如下:

-
构建token-level的pair conditioning input: {z_i_j}
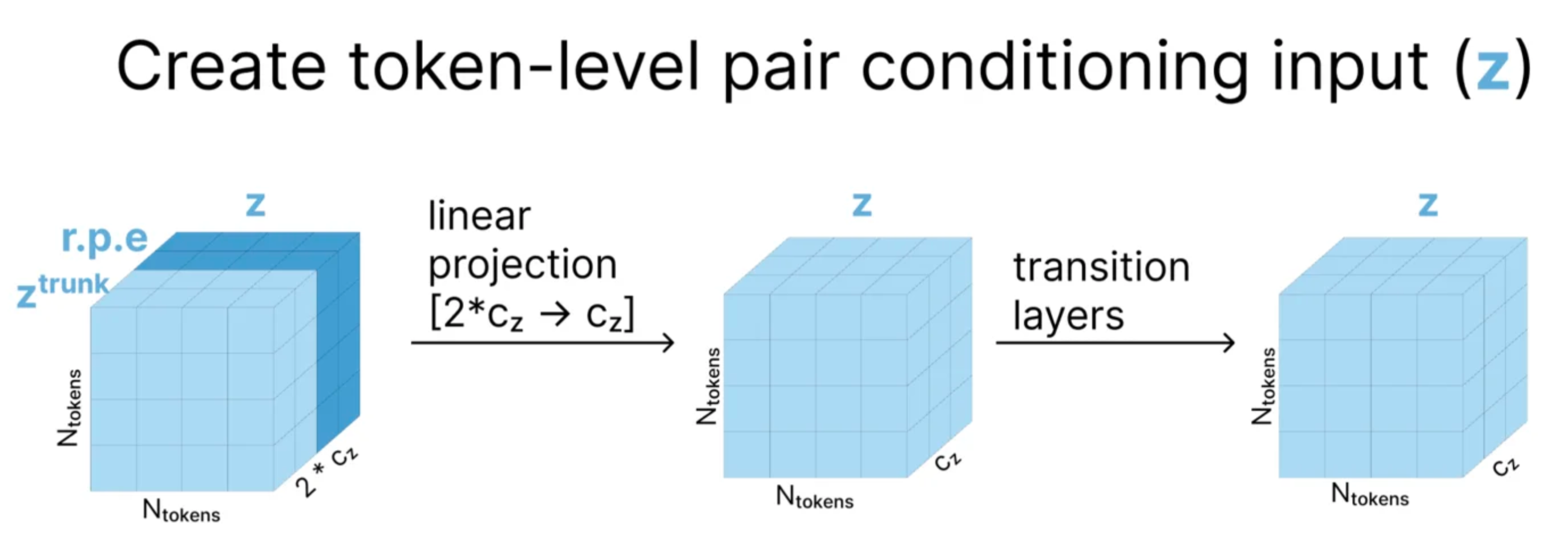
- 首先利用f计算相对位置编码,这个相对位置编码是(i,j)的函数,代表任意两个token之间的相对位置关系,得到结果的维度是c_z;和z_trunk_i_j(维度也是c_z)进行拼接,得到z_i_j,维度是2c_z。
- 然后将z_i_j进行layerNorm,之后再进行线性变换,变换到c_z的维度上。
- 最后经过两次Transition Layer的加合,得到一个新的z_i_j。
-
构建token-level的single conditioning input: {s_i}
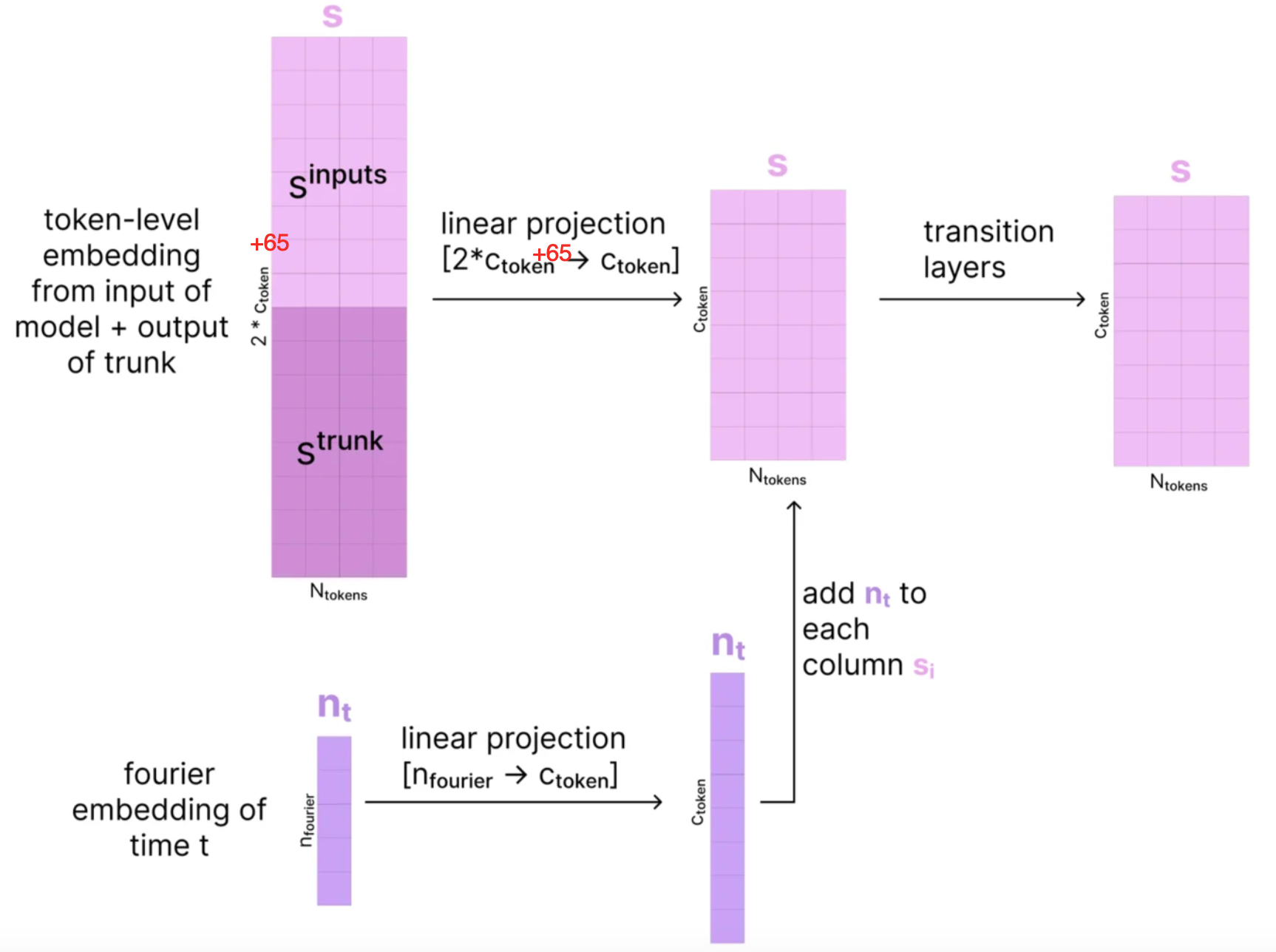
- 首先将s_trunk_i和s_inputs_i这两个single representation拼接起来,得到s_i,维度变成2*c_s+65(s_inputs_i的维度为c_s+65)。
- 然后对s_i进行归一化,然后进行线性变换,维度变成c_s。
- 然后对diffusion的时间步长(具体实际上就是当前时间步的noise schecule的值)信息(标量),将其映射到高维向量空间,以增强模型捕获时间步长非线性特征的能力。
-
具体的伪代码如下所示:

- 生成c维度的向量,每一维都是独立正态分布,得到w和b。
-
生成时间步的高维度向量特征,通过cos函数将标量时间步长t编码到一个高维空间中,具体生成的向量可以理解为如下图(x为时间步t,y的不同值为其在高维空间的向量)所示,每一个t切面就是一个t时刻的高维向量。
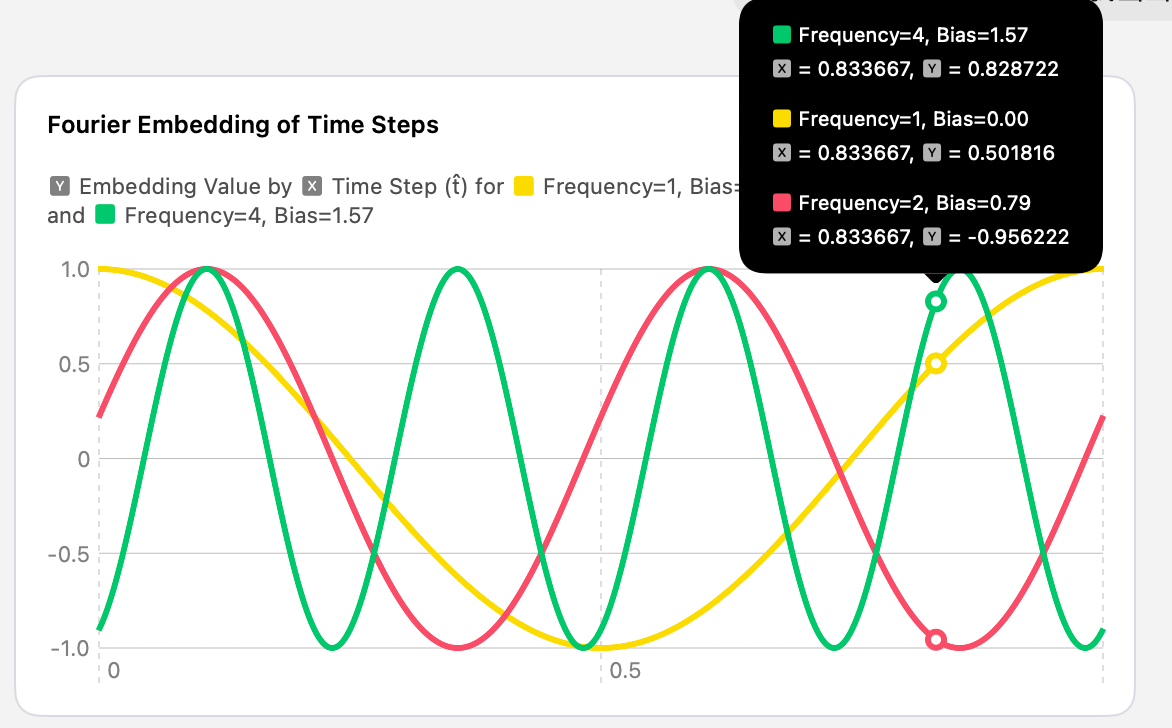
- 不同的频率捕捉了时间步长的多尺度特征(低频表示全局动态,高频表示局部细节)
- 偏移量增加了嵌入的多样性,使模型能学习到更复杂的时间特征。
- 将高维时间步信息先进行归一化,然后进行线性变化后 (n → c_s),加入到token-level 的 single 表征s_i中去了。
- 再经过两次Transition layer的加合,得到一个新的s_i ,维度为c_s。
-
- 通过在此DiffusionCondition部分加入diffusion时间步信息,使得模型在进行de-noising过程中能够知道当前diffusion过程的时间步,并且预测出需要去掉的正确尺度的噪声。
- 经过DiffusionCondition的结果是在token-level尺度上的信息,接下来需要在atom-level计算原子级别的信息。
-
- AtomAttentionEncoder
-
首先将x_noisy_l 进行缩放,转换为单位方差为1的单位向量,其缩放后的结果是一个无量纲的数值,便于保持数值的稳定性。

-
然后正式进入AtomAttentionEncoder函数进行计算:

- AtomAttentionEncoder的输入包括:{f*}(原始特征参考构象特征), {r_noisy_l}(加入当前噪声的当前时间步原子坐标), {s_trunk_i}(经过Pairformer的token-level single表征) , {z_i_j}(经过DiffusionConditioning之后的token-level的Pair 表征)
- AtomAttentionEncoder的输出包括:a_i(token-level的single表征),q_l(本模块计算得到的atom-level的single表征),c_l(基于参考构象获取的atom-level的初始表征), p_l_m(本模块计算得到的atom-level的pair表征)。
-
AtomAttentionEncoder的伪代码如下:(diffusion新增的部分突出显示)

- 首先,从原始参考构象表征中计算得到c_l,并将q_l的初始值设定为c_l,然后然后从参考构象表征中计算atom-level的pair表征p_l_m。
- 接着,然后单r_l不为空的时候(就是当前diffusion部分的推理过程时):
-
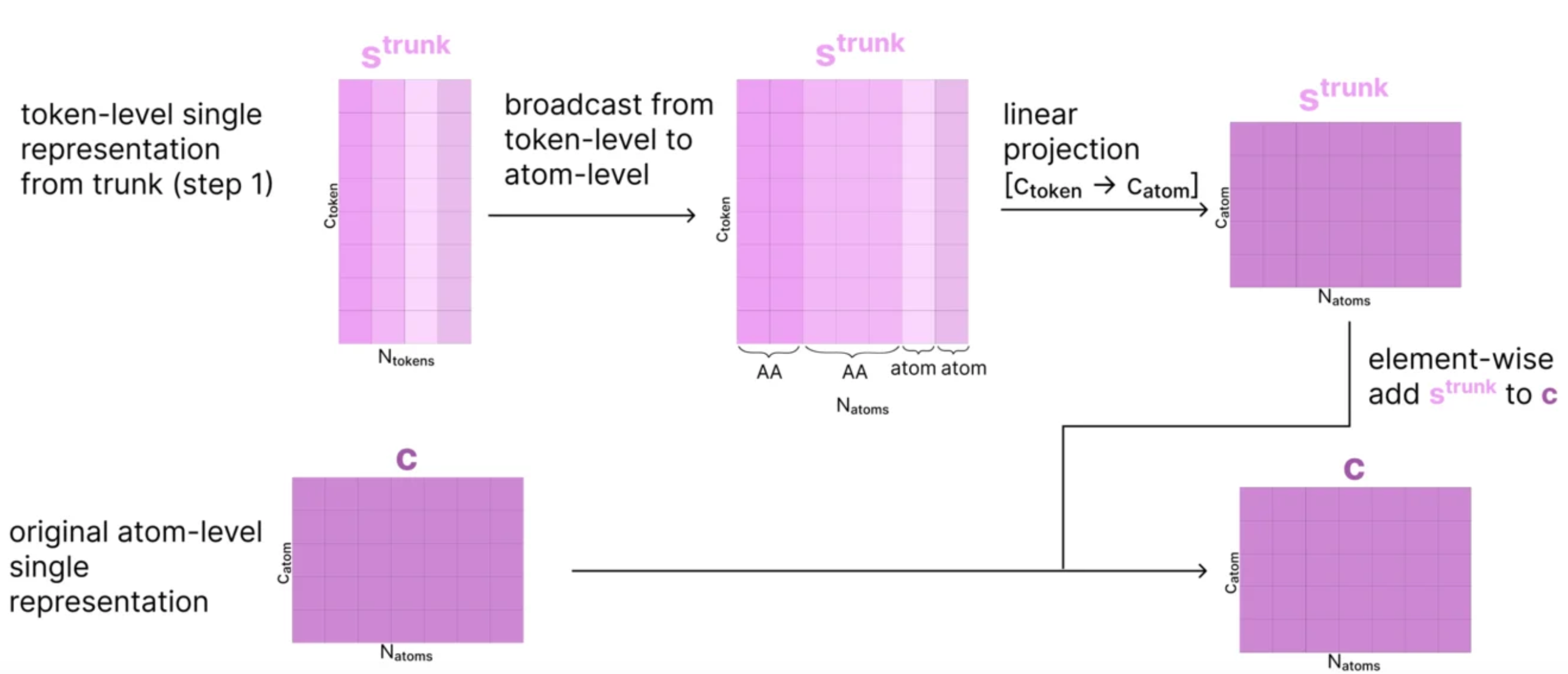
使用s_trunk这个token-level的single特征,获取其在atom序号l对应的token序号tok_idx(l),然后获取这个token序号对应的s_trunk的向量,维度为c_s(c_token),然后进行LayerNorm之后,进行线性变换,维度从c_s → c_atom。然后再加上c_l本身,得到新的c_l,具体过程如下所示:
-
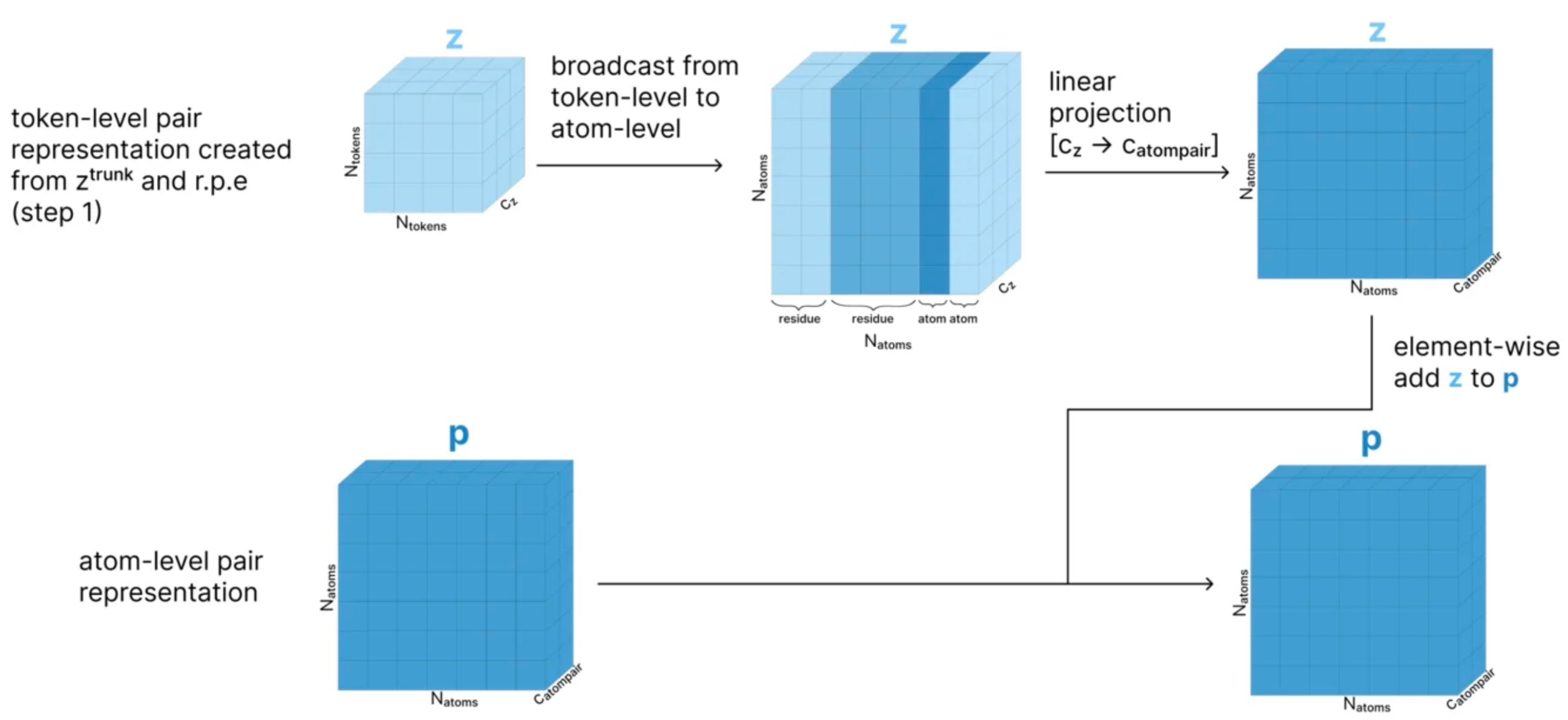
使用z这个token-level的pair特征,获取atom序号l和m的对应的token序号tok_idx(l)和tok_idx(m),然后获取这个两个维度序号对应的z的向量,维度为c_z,然后进行LayerNorm之后,进行线性变换,维度从c_z → c_atompair。最后再加上p_l_m本身,得到新的p_l_m,具体过程如下所示:
-
针对加入当前噪声的当前时间步原子坐标r_noisy_l,将其进行线性变换之后,维度变换3→c_atom,加合到q_l上,得到最新的q_l结果。
-
- 最后,基于c_l对p_l_m的结果进行更新,将p_l_m经过3层MLP得到行动p_l_m,然后通过AtomTransformer计算得到最新的q_l,最后将q_l这个atom-level的single表征,在不同的token维度上求平均,得到a_i(token-level 的single表征)的结果。于是,通过AtomAttentionEncoder就得到以下结果:
- {q_l}:更新之后的atom-level的single表征,包含了当前atom的坐标信息。
- {c_l}:atom-level的single表征,基于Pairformer的token-level single表征更新过的变量,主要起的作用是基于Trunk进行conditioning。
- {p_l_m}: atom-level的pair表征,用于后续的diffusion的conditioning。
- {a_i}:token-level的single表征,从q_l中聚合而来。同时包含了atom-level的坐标信息和token-level的序列信息。
-
- DiffusionTransformers
-
具体的伪代码如下所示:这一部分主要是对上一步计算出来的token-level的信息a_i(其包含了原子三维坐标信息和序列信息)进行self-attention。
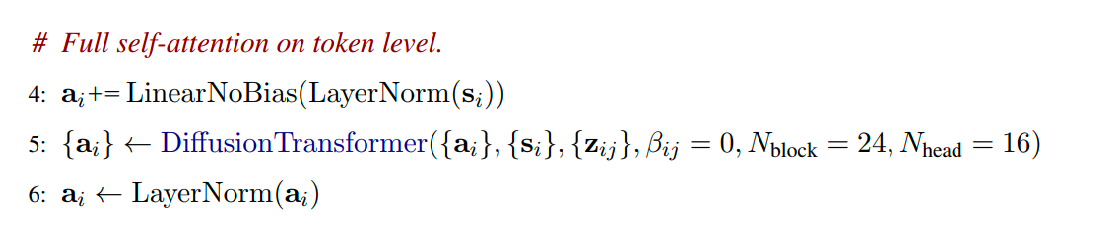
- 首先,对从DiffusionConditioning计算得到的token-level single表征{s_i}出发,计算它的LayerNorm结果之后,在进行线性变换,将其变换到a_i的维度,线性变换维度为 c_token → c_s,然后在加上{a_i}本身进行element-wise add,得到新的{a_i}。
-
然后,对token-level的信息{a_i}进行attention,并且使用从DiffusionConditioning计算得到的{s_i}和{z_i_j}进行conditioning,注意这里的DiffusionTransformer和在之前的所有DiffusionTransformer的一个大的区别是,这里是针对token-level的(Token-level equivalent of the atom transformer),所以这里的 $\beta_{ij} = 0$ 表示不加入稀疏attention的偏置。下面也给出一个示意图:
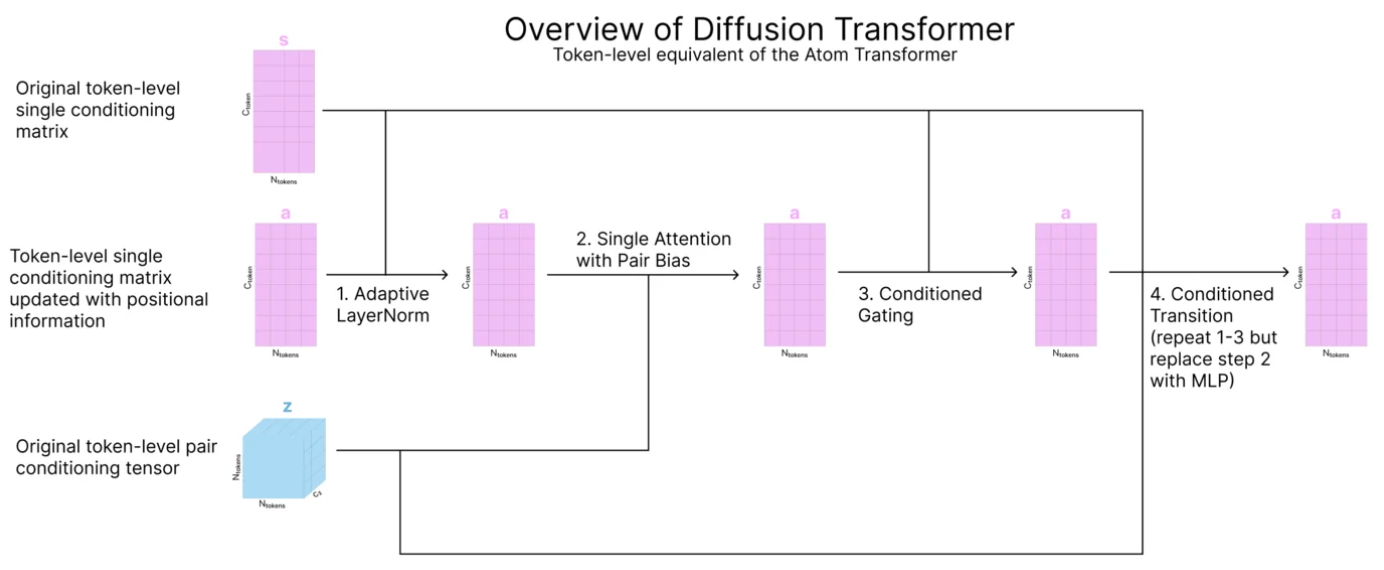
- 最后,a_i经过一个LayerNorm并进行输出,维度为 c_token。
-
-
AtomAttentionDecoder
伪代码如下:

-
最后,我们返回到Atom空间,使用更新之后的 a_i 来将其广播到每一个atom上,以更新atom-level的single表征 q_l。

-
然后,使用Atom Transformer来更新q_l。
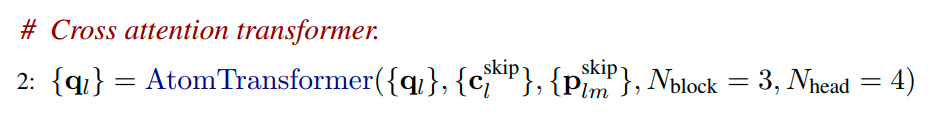
-
最后,将更新后的q_l经过LayerNorm和线性变换之后,映射到原子序列的三维坐标上,得到r_update_l。

-
最后的最后,在AtomAttentionDecoder之外,将“无量纲(dimensionles)”的r_update_l,重新rescale到非单位标准差的 x_out_l上去,返回的就是x_denoised_l。
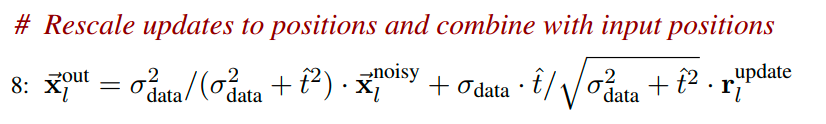
-
Loss Function
最终的LossFunction的公式如下:
$\mathcal{L}_{\text{loss}} = \alpha_{\text{confidence}} \cdot L_{\text{confidence}} + \alpha_{\text{diffusion}} \cdot \mathcal{L}_{\text{diffusion}} + \alpha_{\text{distogram}} \cdot \mathcal{L}_{\text{distogram}}$
其中, $L_{confidence}= \mathcal{L}_{\text{plddt}} + \mathcal{L}_{\text{pde}} + \mathcal{L}_{\text{resolved}} + \alpha_{\text{pae}} \cdot \mathcal{L}_{\text{pae}}$
$\mathcal{L}_{\text{loss}} = \alpha_{\text{confidence}} \cdot \left( \mathcal{L}_{\text{plddt}} + \mathcal{L}_{\text{pde}} + \mathcal{L}_{\text{resolved}} + \alpha_{\text{pae}} \cdot \mathcal{L}_{\text{pae}} \right) + \alpha_{\text{diffusion}} \cdot \mathcal{L}_{\text{diffusion}} + \alpha_{\text{distogram}} \cdot \mathcal{L}_{\text{distogram}}$
- L_distogram: 用于评估预测出来的 token-level 的 distogram(也就是token-token之间的距离)是否准确。
- L_diffusion: 用于评估预测出来atom-level 的 distogram (也就是atom-atome之间的关系)是否准确,同时还包含了一些额外的terms,包括优先考虑就近原子之间的关系以及对蛋白质-配体之间的键的原子进行处理。
- L_confidence: 用于评估模型的关于对自己预测出来的结构哪些是准确或者不准确的self-awareness的准确性。
$L_{distogram}$
- 尽管输出的结果是一个atom-level的三维坐标,但是这里的L_distogram这个loss是一个token-level的指标,表征了模型对token和token之间的距离预测的准确度,但是由于得到的是原子三维坐标,所以要计算token的三维坐标,是直接拿这个token的中心原子的三维坐标作为token的三维坐标。
- 为什么是要评估token(或者原子)之间的距离预测的是否准确,而不是直接评估token(或原子)的坐标预测的是否准确?→ 最本质的原因在于token(或者原子)的坐标在空间中睡着整个结构的旋转或者平移是可能改变的,但是他们之间的相对距离是不会改变的,这样的loss才能够体现结构的旋转和平移不变性。
-
具体的公式是怎么样的?
$\mathcal{L}_{\text{dist}} = -\frac{1}{N_{\text{res}}^2} \sum_{i,j} \sum_{b=1}^{64} y_{ij}^b \log p_{ij}^b$
- 这里y_b_i_j指的是将第i个token和第j个token之间的距离均匀划分到64个桶中去(从2埃到22埃),y_b_i_j指的就是在这64个桶中的某一个桶,这里y_b_i_j使用one-hot编码表示实际的结果落到某一个特定的桶中。
- p_b_i_j指的是对第i个token和第j个token之间的距离的值落到某一个桶中的概率,是一个softmax之后的结果。
- 对于任意一个token对(i,j),求其预测距离和实际距离之间的差别,采用cross-entropy的方式:
- 计算 $\sum_{b=1}^{64} y_{ij}^b \log p_{ij}^b=\log p_{ij}^{\text{target_bin}}$
- 对于所有的token对,计算los的平均值:
- 计算 $-\frac{1}{N_{\text{res}}^2} \sum_{i,j} \log p_{ij}^{\text{target_bin}}$ ,得到最后的L_distogram的loss的值。
$L_{diffusion}$
-
Diffusion的训练过程:(图中红框部分表示Diffusion的训练设置,这幅图表示的是AlphaFold3的总体训练设置,注意忽略了distogram loss部分)
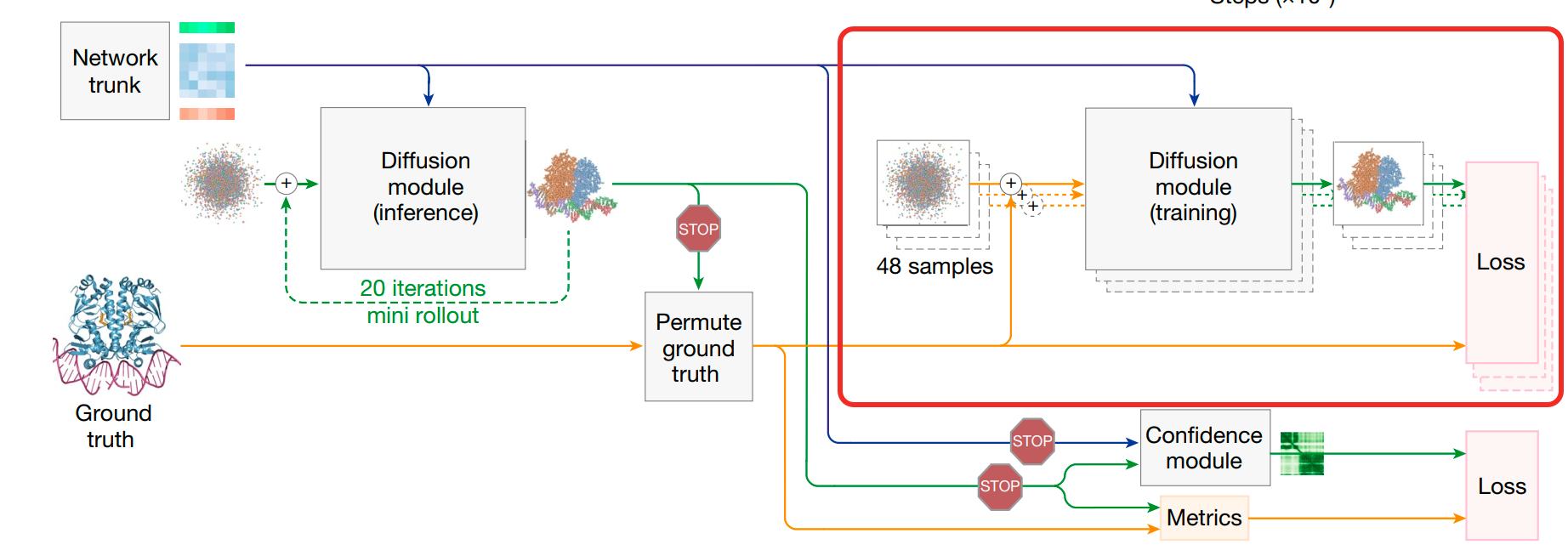
- 在diffusion的训练过程中,其首先使用trunk的输出结果作为输入,包括原始原子特征f*,更新后的token-level pair表征,token-level single 表征等。
- 在训练过程中,Diffusion部分会使用相比于trunk部分更大的batch_size,每个样本通过trunk模块后,会生成48个相关但不同的三维结构作为diffusion模块的输入。这些结构都基于真实结构(来自于训练样本的真实三维结构)生成,但会进行随机旋转和平移,并添加不同程度的噪声。这样的做法是为了获得大量的(加噪结构,目标结构)对,让扩散模型学会如何去噪。
- 由于加噪的大小是随机的,相当于生成了一个从t时间步(属于[0,T],基于噪声大小的不同,t可能是接近于T-1时间步,也可能是接近于0时间步)的带噪声结构,然后希望模型经过一次diffusion module的更新后,接近T时间步,也就是完全没有噪声的状态。
- 最后,对于这48个不同的结果,将其和Ground Truth结果进行对比,计算 loss(L_diffusion),并反向传播,优化模型(这里是仅仅优化diffusion module还是也会优化trunk module?)的参数。
-
Diffusion的loss函数构造:注意这里其实是在原子层面进行loss函数计算。
- $L_{MSE}$:用于计算目标原子坐标和预测原子坐标差值的weighted Mean Squared Error。这里已知目标用于三维坐标的原子序列:{x_GT_l},已知预测三维坐标原子序列{x_l},计算这两个三维结构之间的差别,具体的计算方法如下:
-
先对目标三维结构进行一次刚性对齐,相当于把两个结构整体的位置和方向对齐,让两者在同一个参考坐标系下面进行比较,这样比较的误差就是结构本身的差异,而不是旋转或者位置偏移造成的。这也就解释了,前面计算L_distogram的时候,在没有进行刚性对齐的情况下,直接比较的是token之间的距离在真实值和预测值之间差异,而不是直接比较token的坐标的差异。
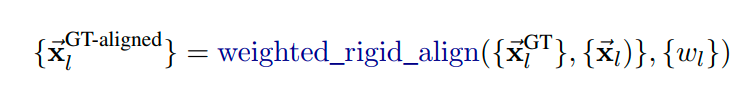
- 然后计算L_mse的值: $L_{MSE} = \frac{1}{3} \cdot \text{mean}_l \big( w_l | \tilde{x}_l - x_l^{GT-aligned} |^2 \big)$
- 注意这里是一个weighted Mean Squared Error: $w_l = 1 + f_l^{\text{is_dna}} \alpha^{\text{dna}} + f_l^{\text{is_rna}} \alpha^{\text{rna}} + f_l^{\text{is_ligand}} \alpha^{\text{ligand}}$ ,其中 $\alpha^{\text{dna}} = \alpha^{\text{rna}} = 5, \alpha^{\text{ligand}} = 10$ 。这里对RNA/DNA和ligand的权重设置的较大,意味着如果这些原子的预测准确性有更高的要求。
-
- $L_{bond}$ :用于确保配体(ligand)和主链之间的键长是合理的损失函数。
- 为什么需要这个loss呢?原因在于扩散模型可以恢复出一个总体结构正确,但是细节不够精确的模型,比如某一个化学键变得过长或者过短。同时配体就像挂在蛋白质链边上的小饰品,你不希望这个饰品过长或者过短,而蛋白质氨基酸之间的肽键基本长度是稳定的,主链内部原子排列的本身就有比较强的约束。
- 所以这里的计算方法为: $\mathcal{L}_{\text{bond}} = \text{mean}_{(l,m) \in \mathcal{B}} \left( \left| \vec{x}_l - \vec{x}_m \right| - \left| \vec{x}_l^{\text{GT}} - \vec{x}_m^{\text{GT}} \right| \right)^2$ ,这里的 $\mathcal{B}$指的是一系列的原子对(l是起始原子的序号,m是结束原子的序号),代表的是protein-ligand bonds。相当于计算目标键长和真实键长之间的平均差距。
- 本质上也是一个MSE的loss。
- $L_{smooth_LDDT}$:用于比较预测的原子对之间的距离和实际原子对之间距离的差异的loss (Local Distance Difference Test),并且着重关注相近原子之间的距离预测的准确性(Local Distance Difference Test)。
-
具体的计算伪代码为:

- 前两步计算任意两个原子之间的距离,包括预测值和实际值。
- 接下来计算(l,m)原子对的预测距离和实际距离的绝对差值 $\delta_{lm}$。
- 然后计算一个分布在[0,1]之间的评分,这个评分用于衡量 $\delta_{lm}$是否能够通过(Local Distance Difference Test)。
- 这里设置了4次Test,每次Test采用了不同的阈值,如果 $\delta_{lm}$ 在设定的阈值范围内,则可以认为对(l,m)这个原子对距离的预测通过了Test,那么这次的Test的评分就会大于0.5,否则不通过小于0.5.
-
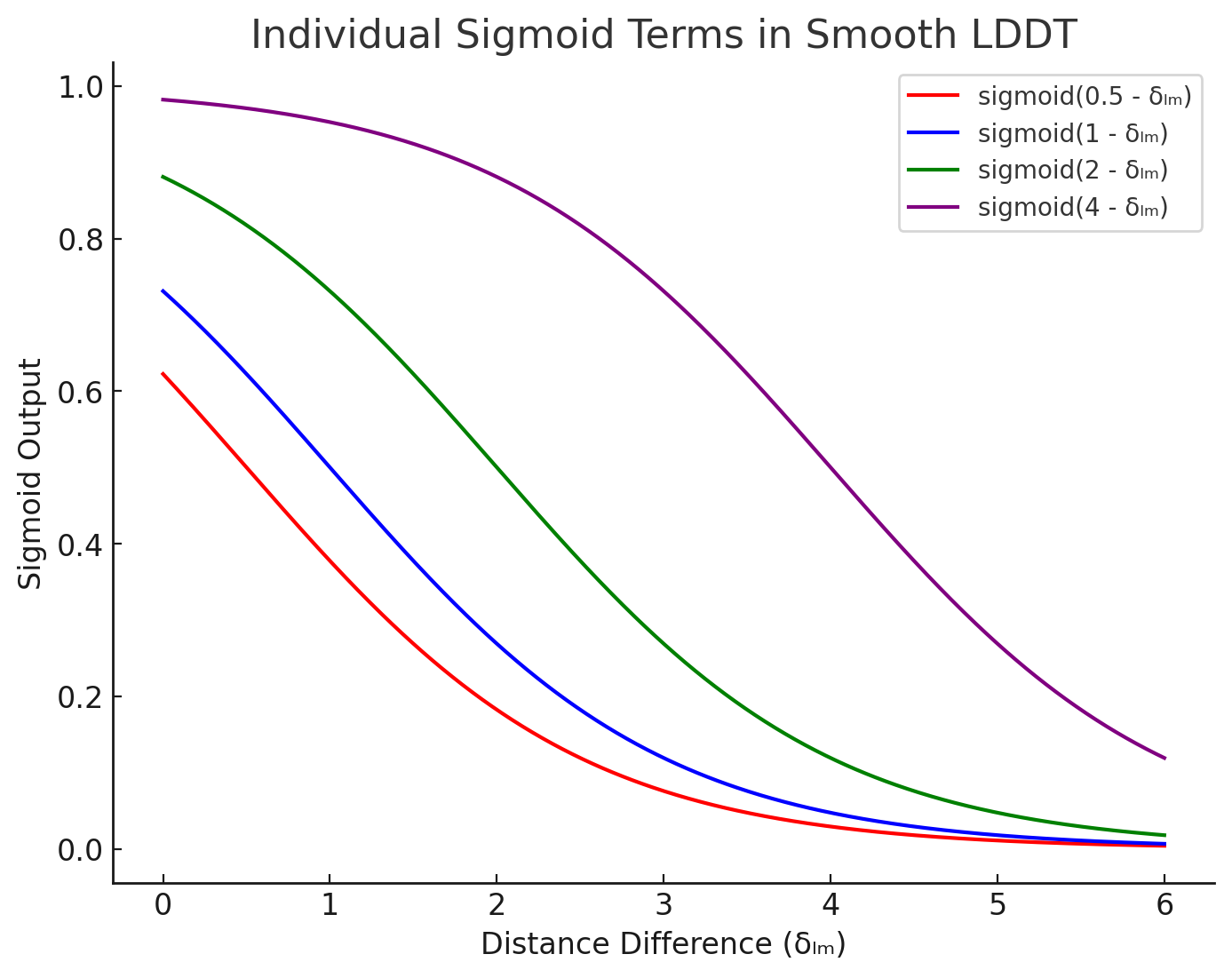
所以每次Test设置了不同的阈值(分别为4, 2, 1, and 0.5 Å),采用sigmoid函数来实现:sigmoid(阈值 - $\delta_{lm}$ ),下面画出了这四个Test的函数曲线:
-
然后对这四个Test的结果进行平均,得到评分 $\epsilon_{lm}$,这是这个评分的曲线,你会发现越靠近0,这个评分越接近于1,否则越接近于0.
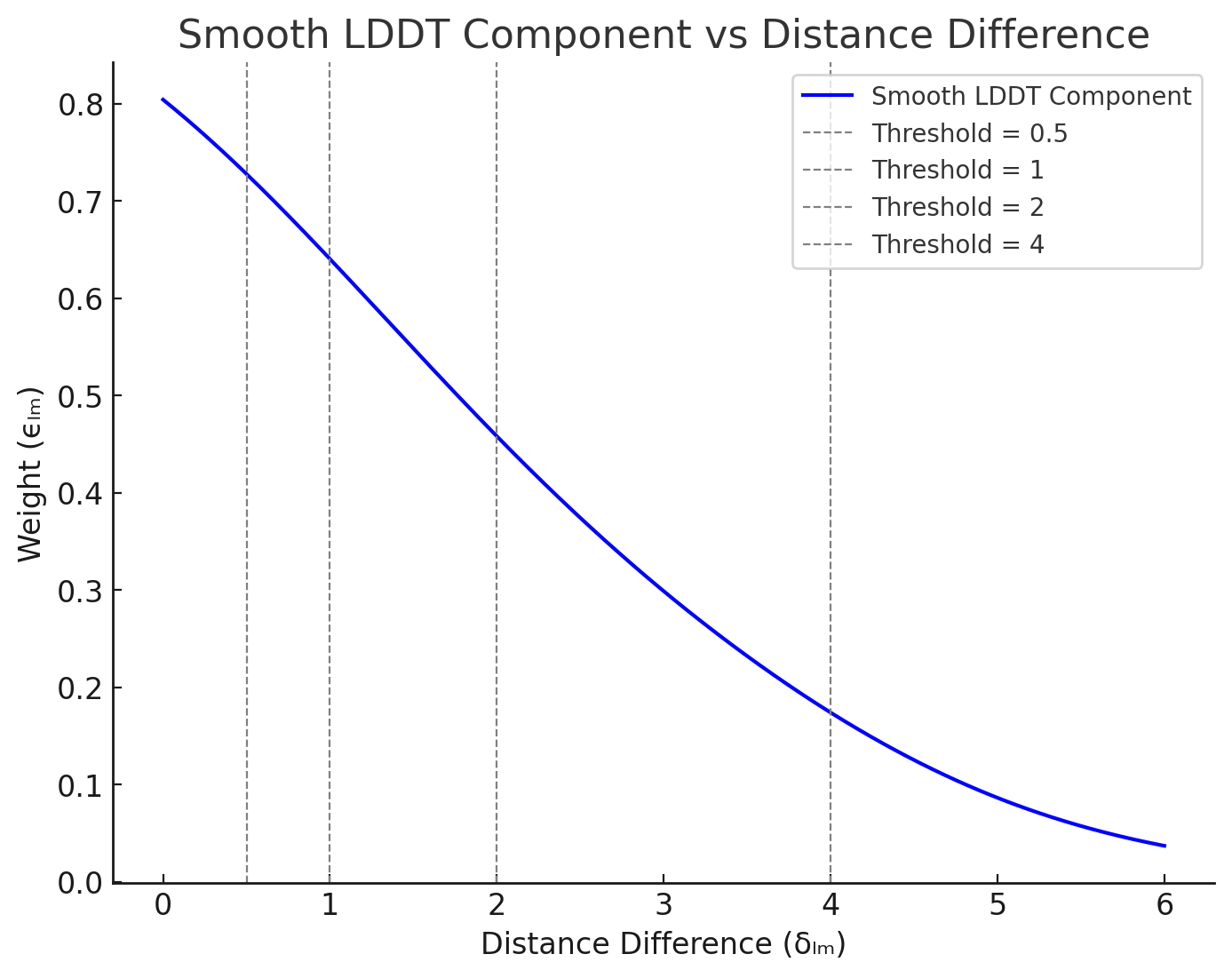
- 然后,为了让这个计算分数主要考察的是相近原子之间的距离,所以对那些实际距离非常远的原子对,不加入到loss的计算(c_l_m=0)。即针对实际距离大于30Å的核苷酸原子对以及实际距离大于15Å的非核苷酸原子对不计入在内。
- 最后,计算那些c_l_m不为0的原子对的$\epsilon_{lm}$评分的均值做为lddt的值,这个值越接近于1,则平均原子对预测的越准。将其换算成loss,为1-lddt。
-
- 最后的最后,$\mathcal{L}_{\text{diffusion}} = \frac{\hat{t}^2 + \sigma_{\text{data}}^2}{(\hat{t} + \sigma_{\text{data}})^2} \cdot \left( \mathcal{L}_{\text{MSE}} + \alpha_{\text{bond}} \cdot \mathcal{L}_{\text{bond}} \right) + \mathcal{L}_{\text{smooth_lddt}}$
- 这里的 $\sigma_{data}$ 是一个常数,由数据的方差决定,这里取16。
- 这里的t^是在训练时的sampled noise level,具体的计算方法是 $\hat{t}=\sigma_{\text{data}} \cdot \exp\left( -1.2 + 1.5 \cdot \mathcal{N}(0, 1) \right)$
- 这里的 $\alpha_{bond}$ 在初始训练的时候是0,在后面fine-tune的时候是1.
- $L_{MSE}$:用于计算目标原子坐标和预测原子坐标差值的weighted Mean Squared Error。这里已知目标用于三维坐标的原子序列:{x_GT_l},已知预测三维坐标原子序列{x_l},计算这两个三维结构之间的差别,具体的计算方法如下:
$L_{confidence}$
- 最后一种loss的作用并不是用来提升模型预测结构的准确性,而是帮助模型学习如何评估自身预测的准确性。这个loss也是四种不同用于评估自身准确性loss的一个加权和。
- 具体的公式如下: $L_{confidence}= \mathcal{L}_{\text{plddt}} + \mathcal{L}_{\text{pde}} + \mathcal{L}_{\text{resolved}} + \alpha_{\text{pae}} \cdot \mathcal{L}_{\text{pae}}$
-
Mini-Rollout解释:
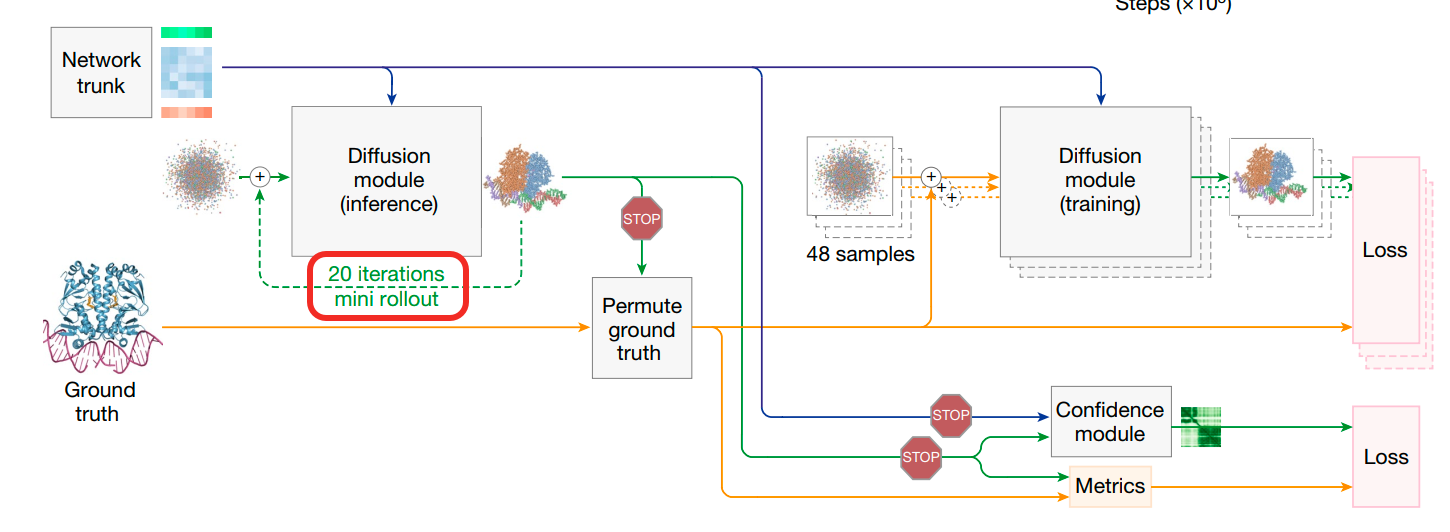
- 原理:正常情况下,要计算模型对生成的三维结构的置信度,需要获取模型最终生成的三维结构进行计算,这与AF2的做法类似。但对于AF3来说,diffusion module单次迭代无法直接生成最终的去噪结果。因此,这里引入了mini-rollout机制:在训练时对Diffusion module进行固定次数(20次)的迭代,从而让模型能从随机噪声快速生成一个近似的蛋白质结构预测。然后利用这个临时预测来计算评估指标和训练confidence head。
- 梯度阻断:注意这里的mini-rollout并不回传梯度(如图中红色STOP标识。不用于优化Diffusion模块也不用于优化Network trunk模块),因为计算L_confidence的主要目标是优化模型对生成结构质量的评估能力,即优化confidence module本身的性能。这种设计确保了diffusion模块的训练目标(单步去噪)和confidence head的训练目标(结构质量度量)相互独立,避免了训练目标不一致导致的冲突。同时也保证了Trunk模块的训练目标(提供更好的特征表征,为后续结构生成提供丰富且通用的特征表示)和confidence head的训练目标(结构质量度量)能够相互独立。
- 注意,这些confidence loss都只针对PDB数据集使用(不适用于任何蒸馏数据集,蒸馏数据集的结构是预测结构不是真实结构);同时在数据集上进行过滤,只选择过滤分辨率(0.1埃到4埃之间)的真实结构进行confidence loss的训练,为了确保模型能够学习到与真实物理结构接近的误差分布。
- 下面分别详细解释每一个loss的含义:
- Predicted Local Distance Difference Test(pLDDT):每个原子的平均置信度。(注意Alphafold2是每个残基的平均置信度)
- 计算单个原子的LDDT: $lddt_l$(训练时):
- 这里的目标是估计预测结构和真实结构之间的差异,且这里是针对特定原子的一个差异的估计。
-
所以这里的计算公式如下设置:
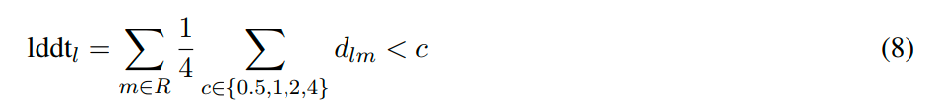
- 其中 $d_{lm}$是mini-rollout的预测的原子l和m之间的距离。
- ${m}\in{R}$ ,m原子的选择是基于此训练序列的真实三维结构来获取:1)m的距离在l的一定就近范围内(30埃或者15埃,取决于m的原子类型);2)m只选择位于聚合物上的原子(小分子和配体不考虑);3)一个token只考虑一个原子,针对标准氨基酸或者核苷酸中的原子,m都是用其代表原子( $C_\alpha$ 或 $C_1$)来表示。
- 然后针对每一对(l,m),进行LDDT(Local Distance Difference Test):$\frac{1}{4} \sum_{c \in {0.5, 1, 2, 4}} d_{lm} < c$,如果l和m在真实距离中比较近,那么他们在预测结果中应该也足够近,这里设置了4个阈值,如果都满足,则LDDT则为1,如果都不满足则为0。
- 最后,相当于针对所有在l附近的m计算得到的LDDT值进行加合,得到一个l原子的$lddt_l$值,其大小可以衡量在l原子上模型的预测结构和真实结构的差异,注意这是一个没有经过归一化的值。
- 计算confidence head输出的此原子的LDDT的概率分布:$p_l^{\text{plddt}}$(训练和预测时)
- 这里暂时忽略具体confidence的计算过程(后续会详细说明),需要知道的是这里的$p_l^{\text{plddt}}$是在l原子处经过confidence head计算得到的,对$lddt_l$值的分布的一个估计。
- 这里$p_l^{\text{plddt}}$是一个50维的向量,将0~100分成了50bin,是一个softmax的结果,预测了$lddt_l$值落在其中特定bin的概率分布。
- 注意这里的计算完全不涉及任何的真实结构,都是基于前面的trunk相关表征进行的预测。
- 计算整个的 $L_{plddt}$(训练时):
- 那么这里这个loss的优化目标就不是最大化 $lddt_l$,而是为了更加准确地预测$lddt_l$。
- 而应该是实际的$lddt_l$值和模型预测的$lddt_l$分布要始终对齐:如果实际的$lddt_l$值低(模型结构预测的不准)那么模型的预测的$lddt_l$ 的分布$p_l^{\text{plddt}}$结果中,落在数值较小的bin中的概率就更大;如果实际的$lddt_l$值高(模型结构预测的准)那么模型的预测的$lddt_l$ 的分布$p_l^{\text{plddt}}$结果中,落在数值较大的bin中的概率就更大。
- 所以使用交叉熵loss来对齐这两者的差异,这也就能够保证模型真实的LDDT分布和预测的LDDT分布是尽量一致的: $\sum_{b=1}^{50} \text{lddt}_l^b \log p_l^b$ 。
-
最后,因为要计算整体的loss,所以在所有原子上进行平均,得到最终计算的方法:
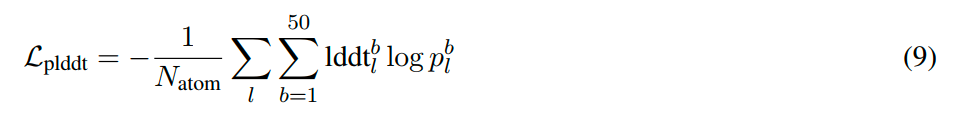
- 计算pLDDT的值(预测时):
- 另外,在预测的时候,模型输出的单个原子的pLDDT的值时,计算方式为:$p_l^{\text{plddt}} * V_{bin}$,得到一个0~100之间的标量,代表了模型对当前位置l原子的lddt的一个预测值。当这个原子周边的原子和它距离都比较近的时候lddt值大,代表模型对当前l原子位置预测的置信度就越高,否则对当前l原子位置预测的置信度就越低。
- 原因在于,经过前面的loss函数的优化,$p_l^{\text{plddt}}$是一个对l原子的预测效果有较好评估能力的分布了。所以就可以相信$p_l^{\text{plddt}}$对lddt分布的估计,可以相当于求期望的方式来求lddt的预测值。
- 计算单个原子的LDDT: $lddt_l$(训练时):
- Predicted Aligned Error(PAE):token对之间的对齐误差的置信度预测(以原子对的距离来计算)。
- 一些概念和方法解释:
- reference frame: 一个token的reference frame使用三个原子的坐标来进行表示: $\Phi_i = (\vec{a}_i, \vec{b}_i, \vec{c}_i)$, 这个frame的作用是用于定义一个token i 的局部参考坐标系,用于与token j 建立联系。针对不同的token,referecne frame的三个原子的选择是不同的:
- 针对蛋白质token,或者残基,其reference frame是:$(\text{N}, \text{C}^\alpha, \text{C})$
- 针对DNA或者RNA的token,其reference frame是: $(\text{C1}’, \text{C3}’, \text{C4}’)$
- 针对其他小分子,其token可能只包含一个原子,那么选择b_i为这个原子本身,然后选择最近的atom为a_i,第二近的atom为c_i。
- 例外:如果选择的三个原子几乎在一条直线上(它们之间的夹脚小于25度),或者在实际的链里找不到这三个原子(比如钠离子只有一个原子),那么这个frame被定义为无效frame,后续不参与计算PAE。
-
$\text{expressCoordinatesInFrame}(\vec{x}, \Phi)$ : 在$\Phi$坐标系下来表示原子$\vec{x}$的坐标。

- 粗略的解释这个算法:
- 首先,从$\Phi$中得到三个参考原子的坐标a,b,c。将b视作新坐标系的原点。
- 然后,从b到a和从b到c的方向,构造一个正交规范基(e_1, e_2, e_3)。
- 最后,将x投影到这个新的基上,得到x_transformed这个在新的坐标系$\Phi$上的坐标。
- 具体的详细解释这个算法:
- 已知三个参考原子的坐标,然后需要以b原子的坐标为原点来构建一个正交的三维坐标系。
- 计算w1和w2,它们是从b到a方向上的一个单位向量和从b到c方向上的一个单位向量。
- 然后计算正交基:
- e1可以看成是位于a和c之间“夹角平分”的一个方向。
- e2是将w1和w2相减之后的一个方向,因为w1和w2都是单位向量,所以这个向量和e1是正交的,而且也在同一个平面上。
- e3是将e2和e1做叉乘,得到与两者都垂直的第三个基向量,从而形成三个完整的正交基。
- 完成这一步后,e1,e2,e3就是一个在以b为原点下的右手系规范正交基。
- 最后将x投影到这个坐标系上面:
- 首先,将x平移,使得b成为原点。
- 然后,进行投影,计算d在每个基向量上的投影,即(de1, de2, d*e3)。
- 最后,就得到了x在坐标系$\Phi$中的新坐标:x_transformed.
- 粗略的解释这个算法:
-
$\text{computeAlignmentError}({\vec{x}_i}, {\vec{x}_i^\text{true}}, {\Phi_i}, {\Phi_i^\text{true}}, \epsilon = 1e^{-8} \, \text{\AA}^2)$:计算token i 和 token j 之间的对齐误差。

- 输入:
- x_i 指的是预测的针对token i 的代表性原子的坐标,x_true_i 指的是真实的token i 的代表性原子的坐标。
- $\Phi_i$指的是预测的针对token i 的reference frame,$\Phi_i^\text{true}$指的是真实的token i 的reference frame。
- 计算流程:
- token对(i, j)之间关系的预测结果:在 token i 的 reference frame 局部坐标系下,计算token j 的代表性原子在这个坐标系中的坐标,相当于计算token j 相对于 token i的相对关系。
- token对(i, j)之间关系的真实结果:在 token i 的 reference frame 局部坐标系下,计算token j 的代表性原子在这个坐标系中的坐标,相当于计算token j 相对于 token i的相对关系。
- 计算对齐误差,即预测的相对位置和真实相对位置之间的差别,使用欧几里得距离来进行计算。如果e_i_j比较小,那么预测的token i 和 j 之间的关系和真实的token i 和 j 之间的关系对齐的好,否则对齐的差。
- 注意,这里的(i,j)是不可交换的,e_i_j和e_j_i是不同的。
- 输入:
- reference frame: 一个token的reference frame使用三个原子的坐标来进行表示: $\Phi_i = (\vec{a}_i, \vec{b}_i, \vec{c}_i)$, 这个frame的作用是用于定义一个token i 的局部参考坐标系,用于与token j 建立联系。针对不同的token,referecne frame的三个原子的选择是不同的:
- PAE Loss 计算流程:
- 通过confidence head计算得到的 $\mathbf{p}_{ij}^{\text{pae}}$ 为 b_pae=64 维度的向量,表示e_i_j 落到64个bin(从0埃到32埃,每0.5埃一个阶梯)中的概率。
- 为了使得 $\mathbf{p}_{ij}^{\text{pae}}$ 的分布更加接近于实际的 e_i_j 的值,采用交叉熵的loss函数来对齐二者,使得$\mathbf{p}_{ij}^{\text{pae}}$能够更好地预测实际的e_i_j的值。(注意:这里loss的设计不是最小化e_i_j的值,那可能是为了获得更好的结构预测精度;而是通过交叉熵loss来更好的让预测的概率$\mathbf{p}_{ij}^{\text{pae}}$和e_i_j的结果更加的接近,从而更好地预测e_i_j的大小;e_i_j越大表明模型认为这两个位置的相对构象存在较大的不确定性,e_i_j越小意味着对于那两个位置的相对构想更有信心)
-
所以最终PAE的loss定义为:(注意这里的e_b_i_j和前面的e_i_j不同,如果e_i_j落在对应的bin b,则这个对应的e_b_i_j是1,否则e_b_i_j是0)
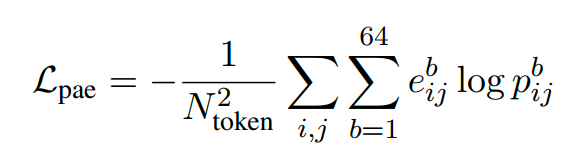
- 如果在预测中要计算PAE_i_j的值,则通过求期望的方式来进行计算。
-
把64个离散的bin取其区间的中心值,然后按照位置乘以每一个位置的预测概率 p_b_i_j(即e_i_j的值落在这个bin中的概率),就得到了对于e_i_j的一个期望的值:
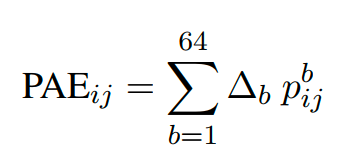
-
- 一些概念和方法解释:
- Predicted Distance Error(PDE):token对之间代表原子绝对距离的置信度预测。
- 除了对齐误差,模型同样也需要预测重要原子之间的绝对距离的预测误差。
- 这里的distance error的计算方式比较简单,如下:
- 首先,计算模型预测的 token i 和token j的代表性原子之间的绝对距离:$d_{ij}^{\text{pred}}$
- 然后,计算模型的真实的 token i 和 token j 的代表性原子之间的绝对距离:$d_{ij}^{\text{gt}}$
- 最后,直接计算二者的绝对差异:$e_{ij}=|d_{ij}^{\text{pred}}-d_{ij}^{\text{gt}}|$
- 类似的,通过confidence head预测出$\mathbf{p}_{ij}^{\text{pae}}$的结果也同样是64维的向量,表示e_i_j 落到64个bin(从0埃到32埃,每0.5埃一个阶梯)中的概率。
-
类似的,然后通过交叉熵loss来对齐二者,得到L_pde:
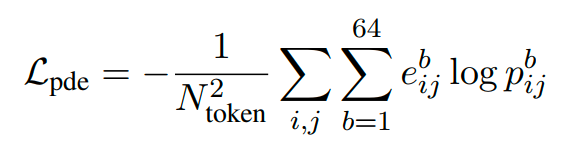
-
类似的,在预测中,使用求期望的方式来求一个token-pair的pde值:($\Delta_b$是区间中心值)
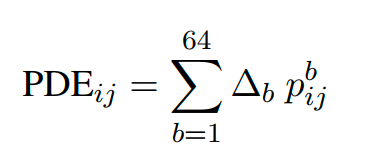
- Experimentally Resolved Prediction:预测一个原子是否能够被实验观测到
- 这个是一个序号为原子序号l的预测置信度值,用于表示当前原子l是否能够正确地被实验观测到。
- y_l 指的是当前的原子是否正确被实验解析,是一个2维的0/1值;p_l是一个从confidence head出来的2维向量,是一个softmax的结果,代表模型预测当前l原子是否被正确解析。
-
最终的优化目标是预测出当前原子是否能够被实验正确解析,所以loss函数是:
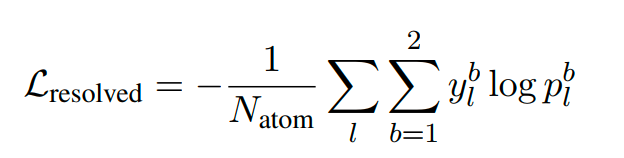
- Predicted Local Distance Difference Test(pLDDT):每个原子的平均置信度。(注意Alphafold2是每个残基的平均置信度)
- Confidence Head 的计算:Confidence Head的目标在于基于前面模型的表征和预测,进一步生成一系列的置信度分布(pLDDT, PAE, PDE, resolved 等的置信度分布),并可以用于后续confidence loss的计算(或者直接用于模型的输出预测)
- Confidence Head的输入:
- 来自最初InputFeatureEmbedder的token-level single embedding 特征 {s_inputs_i}。
- 来自主干网络的token-level single embedding {s_i} 和 token-level pair embedding {z_i_j} 。
- 来自diffusion module的mini-rollout预测结构: {x_pred_l}。
-
算法计算过程解析:

- 对token-level pair embedding z_i_j进行更新,加入了从初始的 single embedding投影过来的信息。
- 计算模型预测出的token i和token j的代表性原子(原子序号为l_rep(i))的三维坐标之间的距离,标识为d_i_j。
- 把d_i_j的值离散到v_bins定义的区间上,计算出其one-hot的表征,然后经过一个线性变换,更新到token-level pair embedding上面。
- 继续让token-level的单体表征{s_i}和配对表征{z_i_j}进行Pairformer的更新,相当于再让这两类表征相互交互强化几轮,得到最终的{s_i}和{z_i_j}。
- 计算PAE的置信度概率,其最终的结果是一个b_pae=64维度的向量。因为PAE实际上也是token-token的表征(虽然实际上计算的是代表原子和frame之间的距离),所以使用{z_i_j}进行线性变换之后直接求softmax来获取这个置信度概率,代表的是其PAE的值落在64个区间中每个区间的概率。(注意:这里i和j是不可交换的)
- 计算PDE的置信度概率,其最终的结果是一个b_pde=64维度的向量。同理,PDE也是token-token的表征(实际上计算的是代表原子之间的绝对距离),使用z_i_j和z_j_i的信息进行融合,然后线性变换并直接求softmax来获取置信度概率,代表的是PDE的值落在64个区间中每个区间的概率。(注意:这里的i和j是可交换的)
- 计算pLDDT的置信度概率(注意:这里的pLDDT的置信度概率是每一个原子的值,是以原子序号l而不是token序号i来进行索引的。)
- 这里s_i(l)代表的含义是:获取原子l所对应的token i 对应的那个token-level single embedding.
- 这里的LinearNoBias_token_atom_idx(l)( … ) ,这个函数的作用是,针对不同的原子l,其对应的用于线性变换的矩阵是不同的,通过token_atom_idx(l)来获取对应的weight矩阵,矩阵形状为[c_token, b_plddt] ,然后将其右乘s_i(l),形状是[c_token]得到最终的向量为[b_plddt]。
- 最后再进行softmax来得到pLDDT的置信度概率,其b_plddt=50,是一个50维度的向量,标识lddt的值落到这个50个bin范围内的概率。
- 计算resolved的置信度概率(注意,这里的resolved的置信度概率也是针对每一个原子的值,同上):计算的结果经过softmax之后是一个2维的向量,预测当前原子是否能够被实验解析出来的置信度。
- Confidence Head的输入:
版权声明:
本文为原创文章,未经授权禁止转载。转载请注明出处:https://shenyichong.github.io/alphafold3-docs/alphafold3-analysis.html